题目内容
某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售量y件之间有如下关系:
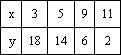
(1)在直角坐标系中
①根据表中提供的数据描出实数对(x,y)的对应点;
②猜测并确定日销售量y件与日销售单价x元之间的函数关系式,并画出图象.并说明当x≥12时对应图象的实际意义.
(2)设经营此商品的日销售利润(不考虑其他因素)为P元,根据日销售规律:
①试求日销售利润P元与日销售单价x元之间的函数关系式;
②当日销售单价x为多少元时,才能获得最大日销售利润?试问日销售利润P是否存在最小值?若有,试求出,并说明其实际意义;若无,请说明理由;
答案:
解析:
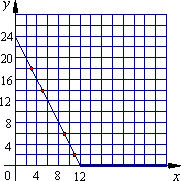
解析:
(1)①四点位置如图所示;
②猜测y是x的一次函数;设y=kx+b,
将(3,18),(5,14)代入上式得:
![]() 解之得:
解之得:![]()
则有y=-2x+24时,再将(9,6),(11,2)代入验证知同样满足;
∴所求函数关系式是y=-2x+24(0≤x<12= 4分
当x≥12时,y=0.
实际意义:当单价大于或等于12元是,销量为0.
画出图象如图所示. 6分

(1)①当0≤x<12时
P=y(x-2)
=(24―2x)(x―2)
=-2x2+28x-48
=―2(x―7)2+50.
当x≥12时,P=0 9分
②由①知,当0≤x<12时
P=―2(x―7)2+50.
∴当x=7时,日销售利润获得最大值为50元.
当x=0时,P=-48,即为最小值.
实际意义:当销售价x=0时,每日亏本48元. 12分

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售量y件之间有如下关系:
某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售量y件之间有如下关系:| x | 3 | 5 | 9 | 11 |
| y | 18 | 14 | 6 | 2 |
①根据表中提供的数据描出实数对(x,y)的对应点;
②猜测并确定日销售量y件与日销售单价x元之间的函数关系式,并画出图象.并说明当x≥12时对应图象的实际意义.
(2)设经营此商品的日销售利润(不考虑其他因素)为 P元,根据日销售规律:
①试求日销售利润P元与日销售单价x元之间的函数关系式;
②当日销售单价x为多少元时,才能获得最大日销售利润?试问日销售利润P是否存在最小值?若有,试求出,并说明其实际意义;若无,请说明理由.
某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售量y件之间有如表所示关系,试确定日销售量y件与日销售单价x元之间的函数关系式.
| x | 3 | 5 | 8 | 10 | 11 |
| y | 18 | 14 | 8 | 4 | 2 |
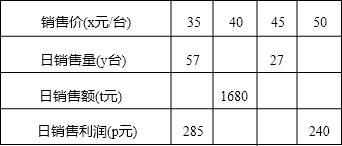 .
. 某商场经营一批进价为2元的小商品,在市场营销中发现此商品的日销售价x(元)与日销售量y(件)之间有如下关系:
某商场经营一批进价为2元的小商品,在市场营销中发现此商品的日销售价x(元)与日销售量y(件)之间有如下关系: