题目内容
27、某商场经营一批进价为2元一件的小商品,在市场营销中发现下商品的日销售单价x元与日销售量y件之间有如下关系:
(1)在所给的直角坐标系①中
1)根据表中提供的数据描出实数对(x,y)的对应点;
2)猜测并确定日销售量y件与日销售单价x元之间的函数关系式,并画出图象.
(2)设经营此商品的日销售利润(不考虑其他因素)为P元,根据日销售规律:
1)试求日销售利润P元与日销售单价x元之间的函数关系式,并求出日销售单价x为多少时,才能获得最大日销售利润.试问日销售利润P是否存在最小值?若有,试求出,若无,请说明理由.
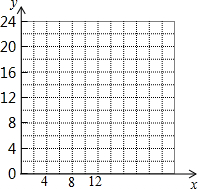
2)在给定的直角坐标系(图2)中,画出日销售利润P元与日销售单价x元之间的函数图象的简图.观察图象,写出x与P的取值范围.
| x | 3 | 5 | 9 | 11 |
| y | 18 | 14 | 6 | 2 |
1)根据表中提供的数据描出实数对(x,y)的对应点;
2)猜测并确定日销售量y件与日销售单价x元之间的函数关系式,并画出图象.
(2)设经营此商品的日销售利润(不考虑其他因素)为P元,根据日销售规律:
1)试求日销售利润P元与日销售单价x元之间的函数关系式,并求出日销售单价x为多少时,才能获得最大日销售利润.试问日销售利润P是否存在最小值?若有,试求出,若无,请说明理由.
2)在给定的直角坐标系(图2)中,画出日销售利润P元与日销售单价x元之间的函数图象的简图.观察图象,写出x与P的取值范围.

分析:(1)根据所描点及趋势,猜测是一次函数,由其中两点可求函数关系式,然后把其它点代入验证得结论;
(2)日销售利润=日销量×每件利润.根据函数关系式运用函数性质结合自变量的取值范围和实际情况求解.
(2)日销售利润=日销量×每件利润.根据函数关系式运用函数性质结合自变量的取值范围和实际情况求解.
解答:解:(1)
①描点.
②猜测它是一次函数y=kx+b.
由两点(3,18)、(5,14)代入上式
解方程组可得k=-2,b=24,
则有y=-2x+24.把(9,6)、(11,2)代入知同样满足,
∴所求为y=-2x+24.
由实际意义知所求应为y=-2x+24 (0≤x<12)和y=0 (x≥12)
(2)①因为销售利润=售价-进价,
则P=xy-2y=y(x-2)=(24-2x)(x-2)=-2x2+28x-48=-2(x-7)2+50
当x=7时,日销售利润获得最大值为50元;
当x>12时,即售价大于12元时,
此时无人购买,所以此时利润P=0 (x≥12).
由实际意义知,当销售价x=0时,即亏本卖出,此时利润P=-48,即为最小值.

②根据实际意义,有0≤x<2时,亏本卖出;
当x=2或x=12时,利润P=0;当x>12时,即高价卖出无人购买P=0.
故作出如上图象.由图象知:x≥0,-48≤P≤50.
①描点.

②猜测它是一次函数y=kx+b.
由两点(3,18)、(5,14)代入上式
解方程组可得k=-2,b=24,
则有y=-2x+24.把(9,6)、(11,2)代入知同样满足,
∴所求为y=-2x+24.
由实际意义知所求应为y=-2x+24 (0≤x<12)和y=0 (x≥12)
(2)①因为销售利润=售价-进价,
则P=xy-2y=y(x-2)=(24-2x)(x-2)=-2x2+28x-48=-2(x-7)2+50
当x=7时,日销售利润获得最大值为50元;
当x>12时,即售价大于12元时,
此时无人购买,所以此时利润P=0 (x≥12).
由实际意义知,当销售价x=0时,即亏本卖出,此时利润P=-48,即为最小值.

②根据实际意义,有0≤x<2时,亏本卖出;
当x=2或x=12时,利润P=0;当x>12时,即高价卖出无人购买P=0.
故作出如上图象.由图象知:x≥0,-48≤P≤50.
点评:(1)猜测求解后需验证.(2)结合图象及实际意义回答问题.

练习册系列答案
相关题目
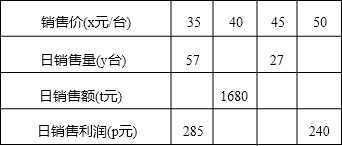
 某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售量y件之间有如下关系:
某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售量y件之间有如下关系:| x | 3 | 5 | 9 | 11 |
| y | 18 | 14 | 6 | 2 |
①根据表中提供的数据描出实数对(x,y)的对应点;
②猜测并确定日销售量y件与日销售单价x元之间的函数关系式,并画出图象.并说明当x≥12时对应图象的实际意义.
(2)设经营此商品的日销售利润(不考虑其他因素)为 P元,根据日销售规律:
①试求日销售利润P元与日销售单价x元之间的函数关系式;
②当日销售单价x为多少元时,才能获得最大日销售利润?试问日销售利润P是否存在最小值?若有,试求出,并说明其实际意义;若无,请说明理由.
某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售量y件之间有如表所示关系,试确定日销售量y件与日销售单价x元之间的函数关系式.
| x | 3 | 5 | 8 | 10 | 11 |
| y | 18 | 14 | 8 | 4 | 2 |
 .
. 某商场经营一批进价为2元的小商品,在市场营销中发现此商品的日销售价x(元)与日销售量y(件)之间有如下关系:
某商场经营一批进价为2元的小商品,在市场营销中发现此商品的日销售价x(元)与日销售量y(件)之间有如下关系: