题目内容
【题目】如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是_________

【答案】5
【解析】
如图,分别延长AC、BD交于点H,易证四边形CPDH为平行四边形,根据平行四边形的性质可得CD与HP互相平分,可得 G正好为PH中点,即在P的运动过程中,G始终为PH的中点,所以G的运行轨迹为△HAB的中位线MN.由此即可求解.
如图,分别延长AC、BD交于点H,
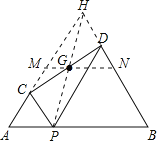
∵∠A=∠DPB=60°,
∴AH∥PD,
∵∠B=∠CPA=60°,
∴BH∥PC,
∴四边形CPDH为平行四边形,
∴CD与HP互相平分.
∵G为CD的中点,
∴G正好为PH中点,即在P的运动过程中,G始终为PH的中点,所以G的运行轨迹为△HAB的中位线MN.
∴MN=![]() AB=5,即G的移动路径长为5.
AB=5,即G的移动路径长为5.
故答案为:5.

练习册系列答案
相关题目
【题目】一次安全知识测验中,学生得分均为整数,满分10分,这次测验中,甲,乙两组学生人数都为5人,成绩如下(单位:分):
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | |
甲 | ______________ | 8 | 8 |
乙 | ______________ | 9 | ______________ |
(2)已知甲组学生成绩的方差![]() ,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定.
,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定.