题目内容
【题目】如图,在△ABC中,点D为BC边的中点,以D为顶点的∠EDF的两边分别与AB、AC交于点E、F,且∠EDF与∠A互补.
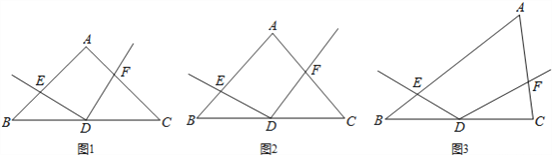
(1)如图①,若AB=AC,且∠A=90°,证明:DE=DF;
(2)如图②,若AB=AC,那么(1)中的结论是否成立?请说明理由.
(3)如图③,若![]() ,探索线段DE与DF的数量关系,并证明你的结论.
,探索线段DE与DF的数量关系,并证明你的结论.
【答案】(1)见解析;(2)成立,理由见解析;(3)![]() ,理由见解析
,理由见解析
【解析】分析:(1)首先根据等腰三角形的性质可得∠DAB=∠DAC=![]() ∠BAC,AD⊥BC,再证明∠C=∠B=45°,∠ADE=∠FDC,AD=DC可以利用ASA定理证明△AED≌△CFD,进而得到DE=DF;
∠BAC,AD⊥BC,再证明∠C=∠B=45°,∠ADE=∠FDC,AD=DC可以利用ASA定理证明△AED≌△CFD,进而得到DE=DF;
(2)DE=DF依然成立.如图2,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,则∠EMD=∠FND=90°,由于AB=AC,点D为BC中点,根据三角形的性质三线合一得到AD平分∠BAC,于是得到DM=DN,在四边形AMDN中.,∠DMA=∠DNA=90°,得到∠MAN+∠MDN=180°,又由于∠EDF与∠MAN互补,证得∠MDN=∠EDF,推出△DEM≌△DFN(ASA),即可得到结论;
(3)结论DE:DF=n:m.如图3,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD同(2)可证∠1=∠2,通过△DEM∽△DFN,得到![]() .由于点E为AC的中点,得到S△ABD=S△ADC,列等积式即可得到结论.
.由于点E为AC的中点,得到S△ABD=S△ADC,列等积式即可得到结论.
详解:(1)DF=DE,
理由:如图1,连接AD,
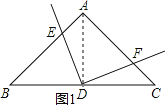
∵Rt△ABC是等腰三角形,
∴∠C=∠B=45°,
∴D是斜边BC的中点,
∴∠DAB=∠DAC=![]() ∠BAC=45°,AD⊥BC,
∠BAC=45°,AD⊥BC,
∴AD=DC,
∵∠EDF=90°,
∴∠ADF+∠ADE=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ADF+∠FDC=90°,
∴∠ADE=∠FDC,
在△ADE和△CDF中,
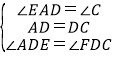 ,
,
∴△AED≌△CFD(ASA);
∴DE=DF;
(2)DE=DF依然成立.
如图2,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,
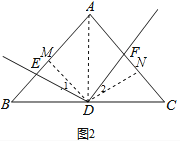
则∠EMD=∠FND=90°,
∵AB=AC,点D为BC中点,
∴AD平分∠BAC,
∴DM=DN,
∵在四边形AMDN中.,∠DMA=∠DNA=90°,
∴∠MAN+∠MDN=180°,
又∵∠EDF与∠MAN互补,
∴∠MDN=∠EDF,
∴∠1=∠2,
在△DEM与△DFN中,
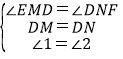 ,
,
∴△DEM≌△DFN(ASA),
∴DE=DF.
(3)结论DE:DF=n:m.
如图3,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,

同(2)可证∠1=∠2,
又∵∠EMD=∠FND=90°,
∴△DEM∽△DFN,
∴![]() .
.
∵点D为BC边的中点,
∴S△ABD=S△ADC,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

【题目】发现问题、探索规律,要有一双敏锐的双眼,下面的图形是由边长为1的小正方形按照某种规律排列而成的.

(1)观察图形,填写下表:
图形个数(n) | (1) | (2) | (3) |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形有 个,周长为 .
(3)写出第30个图形的周长.