Question

如图1，在△ABC中，∠ACB=90°，AC=BC，直线l经过顶点C，过A、B两点分别作l的垂线AE、BF，E、F为垂足．

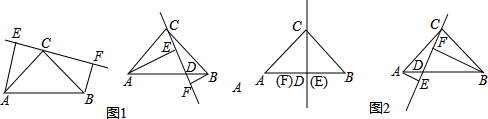
（1）当直线l不与底边AB相交时，求证：EF=AE+BF．
（2）如图2，将直线l绕点C顺时针旋转，使l与底边AB交于点D，请你探究直线l在如下三种可能的位置时，EF、AE、BF三者之间的数量关系．（直接填空）
①当AD＞BD时，关系是：

AE=BF+EF

．
②当AD=BD时，关系是：

AE=BF

．
③当AD＜BD时，关系是：

BF=AE+EF

．

Answer 1

分析：（1）求出∠AEC=∠BFC=90°，∠EAC=∠FCB，根据AAS证△EAC≌△FCB，推出CE=BF，AE=CF即可；
（2）类比（1）证得对应的两个三角形全等，求出线段之间的关系即可．

解答：解：（1）证明：∵AE⊥EF，BF⊥EF，∠ACB=90°
∴∠AEC=∠BFC=∠ACB=90°，
∴∠EAC+∠ECA=90°，∠ECA+∠FCB=90°，
∴∠EAC=∠FCB，
在△EAC和△FCB中，

∠AEC=∠CFB ∠EAC=FCB AC=BC

∴△EAC≌△FCB（AAS），
∴CE=BF，AE=CF，
∴EF=CE+CF=AE+BF，
即EF=AE+BF；

（2）①当AD＞BD时，
∵∠ACB=90°，AE⊥L直线，
∴∠BCF=∠CAE（同为∠ACD的余角），
又∵AC=BC，BF⊥L直线
即∠BFC=∠AEC=90°，
∴△ACE≌△BCF，
∴CF=AE，CE=BF，
∵CF=CE+EF=BF+EF，
∴AE=BF+EF；
②当AD=BD时，
AD=AE，BF=BD，
∵AD⊥AB，AC=BC，AD=AD，
∴Rt△ADC≌Rt△BDC（HL），
∴AD=BD，
∴AE=BF；
③当AD＜BD时，
∵∠ACB=90°，BF⊥L直线，
∴∠CBF=∠ACE（同为∠BCD的余角），
又∵AC=BC，BE⊥L直线，
即∠AEC=∠BFC=90°
∴△ACE≌△BCF，
∴CF=AE，BF=CE，
∵CE=CF+EF=AE+EF，
∴BF=AE+EF．

点评：此题考查三角形全等的判定与性质，以及等量代换等知识点．