题目内容
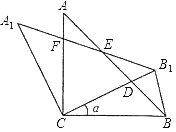
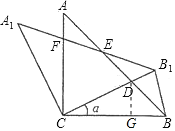
【题目】如图,△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角α(0°<α<90°),连接BB1,设CB1交AB于D,AlB1分别交AB,AC于E,F.
(1)求证:△BCD≌△A1CF;
(2)若旋转角α为30°,
①请你判断△BB1D的形状;
②求CD的长.
【答案】(1)证明见解析;(2)①△BB1D是等腰三角形.②![]() -1.
-1.
【解析】试题分析:
(1)①由AC=BC可得∠A=∠ABC;②由△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C可得:∠A1=∠A,A1C=AC,∠ACA1=∠BCB1=α;①②结合可得:∠A1=∠CBD,A1C=BC,这样由“ASA”可证得△BCD≌△A1CF;
(2)①由CB=CB1,∠BDB1=α+∠CBA,α为30°,证明∠BDB1=∠BBD=75°可得BD=BB1,从而可得△BB1D是等腰三角形;
②过点D作DG⊥BC于点G,设DG=x,则由∠DBC=45°,α为30°可得:BG=x,CD=2x,CG=2-x,然后在Rt△CDG中由勾股定理建立方程解出x的值,即可求得CD的长.
试题解析:
(1)证明:(1)∵AC=BC,
∴∠A=∠ABC.
∵△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C,
∴∠A1=∠A,A1C=AC,∠ACA1=∠BCB1=α.
∴∠A1=∠CBD,A1C=BC.
在△CBD与△CA1F中,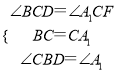 ,
,
∴△BCD≌△A1CF(ASA).
(2)解:①△BB1D是等腰三角形,理由如下:
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°.
又由旋转的性质得到BC=B1C,则∠CB1B=∠CBB1,
∴∠CB1B=∠CBB1=![]() =75°.
=75°.
又∵∠BDB1=∠ABC+α=45°+30°=75°,
∴∠BDB1=∠DB1B=75°,
∴BD=BB1,
∴△BB1D是等腰三角形.
②如图,过D作DG⊥BC于G,设DG=x,
∵ɑ=30°,∠DBE=45°,
∴BG=x,CG=CB-BG=2-x,DC=2x,
又∵在Rt△CDG中,CD2=DG2+CG2,
∴![]() ,解得:
,解得: ![]() (不合题意,舍去),
(不合题意,舍去),
∴CD=2x=![]() .
.

【题目】为了争创全国文明卫生城市,优化城市环境,某市公交公司决定购买10辆全新的混合动力公交车,现有![]() 两种型号,它们的价格及年省油量如下表:
两种型号,它们的价格及年省油量如下表:
型 号 |
|
|
价格(万元/辆) |
|
|
年省油量(万升/辆) | 2.4 | 2 |
经调查,购买一辆![]() 型车比购买一辆
型车比购买一辆![]() 型车多20万元,购买2辆
型车多20万元,购买2辆![]() 型车比购买3辆
型车比购买3辆![]() 型车少60万元.
型车少60万元.
(1)请求出![]() 和
和![]() 的值;
的值;
(2)若购买这批混合动力公交车(两种车型都要有), 每年能节省的油量不低于22.4万升,请问有几种购车方案?(不用一一列出)请求出最省钱的购车方案所需的车款.