Question

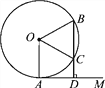
【题目】如图，AM为⊙O的切线，A为切点，BD⊥AM于点D，BD交⊙O于点C，OC平分∠AOB，求∠B的度数．

Answer 1

【答案】∠B＝60°.

【解析】试题分析：由AM为圆O的切线，利用切线的性质得到OA与AM垂直，再由BD与AM垂直，得到OA与BD平行，利用两直线平行内错角相等得到∠AOC＝∠BCO，再由OC为角平分线得到∠BOC＝∠AOC，由OB=OC，利用等边对等角得到∠OCB＝∠B，等量代换得到∠BOC=∠OBC=∠OCB=60°．

试题解析：∵AM切⊙O于点A，∴OA⊥AM.

∵BD⊥AM，∴∠OAD＝∠BDM＝90°，

∴OA∥BD，

∴∠AOC＝∠BCO，

∵OC平分∠AOB，∴∠BOC＝∠AOC，

∵OB＝OC，∴∠OCB＝∠B，

∴∠BOC＝∠OCB＝∠B，故∠B＝60°.