题目内容
【题目】如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离AB.(结果保留小数点后一位,其中 ![]() =1.732)
=1.732)
【答案】解:由题意得,BC=80× ![]() =40(海里),
=40(海里),
由图示可知,∠ACB=60°,
根据平行线的性质得,∠CBF=30°,
则∠ABC=180°﹣60°﹣30°=90°,
∴ ![]() =tan60°,
=tan60°,
则AB= ![]() BC=40
BC=40 ![]() ≈69.3(海里).
≈69.3(海里).
答:此时渔政船距钓鱼岛A的距离AB约为69.3海里.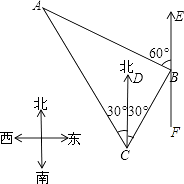
【解析】此题可先由速度和时间求出BC的距离,再由各方向角关系确定△ABC为直角三角形,解此直角三角形即可求得结果.
【考点精析】认真审题,首先需要了解关于方向角问题(指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角).

练习册系列答案
相关题目