Question

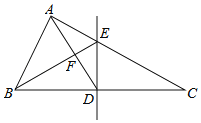
【题目】如图，在△ABC中，BC的垂直平分线分别交BC、AC于点D、E，BE交AD于点F，AB＝AD．

（1）判断△FDB与△ABC是否相似，并说明理由；

（2）BC＝6，DE＝2，求△BFD的面积．

Answer 1

【答案】（1）相似，理由见解析；（2）．

【解析】

（1）根据线段垂直平分线的性质得出BE＝CE，根据等腰三角形的性质得出∠EBC＝∠ECB，∠ABC＝∠ADB，根据相似三角形的判定得出即可；

（2）根据△FDB∽△ABC得出＝＝，求出AB＝2FD，可得AD＝2FD，DF＝AF，根据三角形的面积得出S△AFB＝S△BFD，S△AEF＝S△EFD，根据DE为BC的垂直平分线可得S△BDE=S△CDE，可求出△ABC的面积，再根据相似三角形的性质求出答案即可．

（1）△FDB与△ABC相似，理由如下：

∵DE是BC垂直平分线，

∴BE＝CE，

∴∠EBC＝∠ECB，

∵AB＝AD，

∴∠ABC＝∠ADB，

∴△FDB∽△ABC．

（2）∵△FDB∽△ABC，

∴＝＝，

∴AB＝2FD，

∵AB＝AD，

∴AD＝2FD，

∴DF＝AF，

∴S△AFB＝S△BFD，S△AEF＝S△EFD，

∴S△ABC＝3S△BDE＝3××3×2＝9，

∵△FDB∽△ABC，

∴＝（）2＝（）2＝，

∴S△BFD＝S△ABC＝×9＝．