题目内容
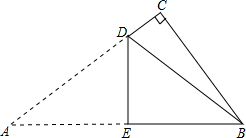 如图,已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,现将△ABC进行折叠,使顶点A、B重合,则△ADB的面积为
如图,已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,现将△ABC进行折叠,使顶点A、B重合,则△ADB的面积为| 75 |
| 4 |
| 75 |
| 4 |
分析:根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
解答:解:在直角△ABC中,
AB=
=
=10(cm).
则AE=AB÷2=5(cm).
设DE=x,
由题意可得出:∠A=∠A,∠AED=∠C,
∴△ADE∽△ABC,
故有
=
;
∴
=
;
解可得x=
,
∴△ADB的面积为:
×
×10=
(cm2).
故答案为:
.
AB=
| AC2+BC2 |
| 62+82 |
则AE=AB÷2=5(cm).
设DE=x,
由题意可得出:∠A=∠A,∠AED=∠C,
∴△ADE∽△ABC,
故有
| AE |
| AC |
| DE |
| BC |
∴
| 5 |
| 8 |
| x |
| 6 |
解可得x=
| 15 |
| 4 |
∴△ADB的面积为:
| 1 |
| 2 |
| 15 |
| 4 |
| 75 |
| 4 |
故答案为:
| 75 |
| 4 |
点评:此题主要考查了翻折变换的性质,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.

练习册系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.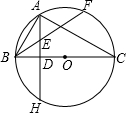 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为