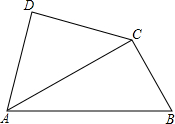
题目内容
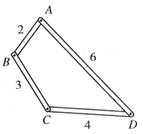
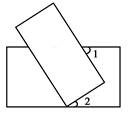
如图,用四个螺丝将四条不可弯曲的木条围成一个木框ABCD,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则现在A、C相对的螺丝的距离的最大值,以及现在B、D相对的螺丝的距离的最大值分别为
A. 5和7 B. 10和7 C. 5和8 D. 10和8

A. 5和7 B. 10和7 C. 5和8 D. 10和8
A
试题分析:若两个螺丝的距离最大,则此时这个木框的形状为三角形,可根据三条木棍的长来判断有几种三角形的组合,然后分别找出这些三角形的最长边即可.
解: ①选2+3、4、6作为三角形,则三边长为5、4、6;6-5<4<6+5,能构成三角形,此时A、C相对的螺丝的距离为5,B、D相对的螺丝的距离小于7;
②选3+4、6、2作为三角形,则三边长为2、7、6;6-2<7<6+2,能构成三角形,此时A、C相对的螺丝的距离小于5,B、D相对的螺丝的距离为7;
③选4+6、2、3作为三角形,则三边长为10、2、3;2+3<10,不能构成三角形,此种情况不成立;
综上所述,A、C相对的螺丝的距离的最大值为5,B、D相对的螺丝的距离的最大值为7
故选A.
点评:能够正确的判断出调整角度后三角形木框的组合方法是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
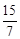

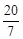
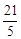
 ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
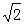 ,P是AC上的一个动点.
,P是AC上的一个动点.