题目内容
如图,在 ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.

(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
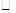 ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
(1)由全等三角形的判定定理AAS证得结论。
(2)由(1)中全等三角形的对应边相等推知点E是边DF的中点,∠1=∠2;根据角平分线的性质、等量代换以及等角对等边证得DC=FC,则由等腰三角形的“三合一”的性质推知CE⊥DF。
(2)由(1)中全等三角形的对应边相等推知点E是边DF的中点,∠1=∠2;根据角平分线的性质、等量代换以及等角对等边证得DC=FC,则由等腰三角形的“三合一”的性质推知CE⊥DF。
分析:(1)由全等三角形的判定定理AAS证得结论。
(2)由(1)中全等三角形的对应边相等推知点E是边DF的中点,∠1=∠2;根据角平分线的性质、等量代换以及等角对等边证得DC=FC,则由等腰三角形的“三合一”的性质推知CE⊥DF。
解:(1)证明:如图,∵四边形ABCD是平行四边形,∴AD∥BC。

又∵点F在CB的延长线上,∴AD∥CF。∴∠1=∠2。
∵点E是AB边的中点,∴AE=BE,
∵在△ADE与△BFE中,
 ,
,∴△ADE≌△BFE(AAS)。
(2)CE⊥DF。理由如下:
如图,连接CE,
由(1)知,△ADE≌△BFE,
∴DE=FE,即点E是DF的中点,∠1=∠2。
∵DF平分∠ADC,∴∠1=∠3。∴∠3=∠2。
∴CD=CF。∴CE⊥DF。

练习册系列答案
相关题目

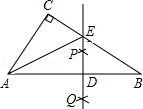
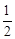 AB的长为半径做弧,两弧相交于点P和Q.
AB的长为半径做弧,两弧相交于点P和Q.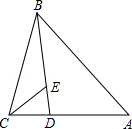

 ,结果精确到0.1海里)
,结果精确到0.1海里)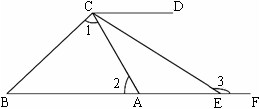
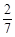 ,求这个正多边形的边数和它一个内角的度数。
,求这个正多边形的边数和它一个内角的度数。 ,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。
,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。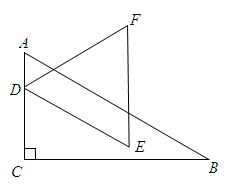
 ,当a=2时,求T的值;
,当a=2时,求T的值;