题目内容
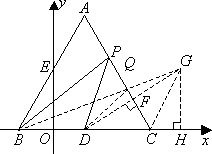
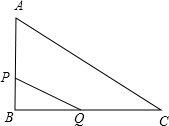
如图,已知:△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴正半轴相交于点E,点B的坐标是(-1,0),P点是AC上的动点(P点与A,C两点不重合).
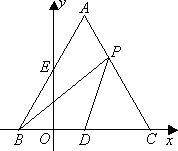
(1)写出点A,点E的坐标.
(2)若抛物线y=-![]() x2+bx+c过A,E两点,求抛物线的解析式.
x2+bx+c过A,E两点,求抛物线的解析式.
(3)连结PB,PD.设l为△PBD的周长,当l取最小值时,求点P的坐标及l的最小值,并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.
答案:
解析:
解析:
|
解:(1)点 (2) 得: 抛物线的解析式是: (3)过 则 再连结 当点 又过 在 设线段 线段 同理可得线段 则此时 此时 理由如下: 把 故此时 (2)小题所求的抛物线
|

练习册系列答案
相关题目
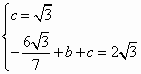 ,
,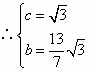 .
.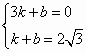 ,
,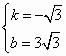 .
.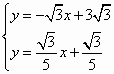 的解,得
的解,得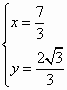 .
.
 如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF.
如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF. 如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.
如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE. 如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则
如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则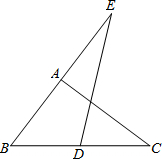 如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,
如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,