题目内容
如图,已知在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始,沿AB边向点B以1cm/S的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,(其中一点到达终点,另一点也停止运动),设经过t秒.(1)如果P、Q分别从A、B两点同时出发,那么几秒后,△PBQ的面积等于△ABC的面积的
| 1 | 3 |
(2)在(1)中,△PQB的面积能否等于10cm2?请说明理由.
(3)若P、Q分别从A、B两点出发,那么几秒后,PQ的长度等于6cm?
(4)P、Q在移动的过程中,是否存在某一时刻t,使得PQ∥AC?若存在求出t的值,若不存在请说明理由.
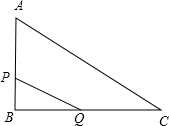
分析:(1)首先表示出AP=t,BQ=2t,PB=AB-AP=6-t,再得出S△PBQ与S△ABC面积,利用S△PBQ=
S△ABC求出即可;
(2)利用S△PBQ=t(6-t),假设等于10,利用根的判别式求出即可;
(3)根据PQ=6,利用勾股定理BP2+BQ2=PQ2,求出即可;
(4)当PQ∥AC时,则△BPQ∽△BAC,得出对应边的关系,再求出t即可.
| 1 |
| 3 |
(2)利用S△PBQ=t(6-t),假设等于10,利用根的判别式求出即可;
(3)根据PQ=6,利用勾股定理BP2+BQ2=PQ2,求出即可;
(4)当PQ∥AC时,则△BPQ∽△BAC,得出对应边的关系,再求出t即可.
解答:解:(1)∵P、Q移动t秒时AP=t,BQ=2t,
则PB=AB-AP=6-t,
∴S△PBQ=
BP•BQ=
(6-t)•2t=t(6-t),
∵S△ABC=
AB•BC=
×6×8=24,
当S△PBQ=
S△ABC时,则t(6-t)=24×
,
t2-6t+8=0,
t1=2,t2=4,
∴当t=2或4时,△PBQ的面积等于△ABC的面积的
.
(2)不存在t的值,得△PQB的面积等于10cm2.
理由:设S△PQB=10,由(1)知:S△PBQ=t(6-t),
∴t(6-t)=10,整理得t2-6t+10=0,
∵△=(-6)2-4×1×10=-4<0,
∴该方程无解,
∴不存在t的值,使得△PQB的面积等于10cm2.
(3)当PQ=6时,在Rt△PBQ中,∵BP2+BQ2=PQ2,
∴(6-t)2+(2t)2=62,
5t2-12t=0,
t(5t-12)=0,
t1=0,t2=
,
∵t=0时不合题意,舍去,
∴当t=
时,PQ的长度等于6cm.
(4)当PQ∥AC时,则△BPQ∽△BAC,
∴
=
,
∴
=
整理得3t=12-2t,
∴t=
,
∴当t=
时,PQ∥AC.
则PB=AB-AP=6-t,
∴S△PBQ=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
当S△PBQ=
| 1 |
| 3 |
| 1 |
| 3 |
t2-6t+8=0,
t1=2,t2=4,
∴当t=2或4时,△PBQ的面积等于△ABC的面积的
| 1 |
| 3 |
(2)不存在t的值,得△PQB的面积等于10cm2.
理由:设S△PQB=10,由(1)知:S△PBQ=t(6-t),
∴t(6-t)=10,整理得t2-6t+10=0,
∵△=(-6)2-4×1×10=-4<0,
∴该方程无解,
∴不存在t的值,使得△PQB的面积等于10cm2.
(3)当PQ=6时,在Rt△PBQ中,∵BP2+BQ2=PQ2,
∴(6-t)2+(2t)2=62,
5t2-12t=0,
t(5t-12)=0,
t1=0,t2=
| 12 |
| 5 |
∵t=0时不合题意,舍去,
∴当t=
| 12 |
| 5 |
(4)当PQ∥AC时,则△BPQ∽△BAC,
∴
| Bp |
| BA |
| BQ |
| BC |
∴
| 6-t |
| 6 |
| 2t |
| 8 |
∴t=
| 12 |
| 5 |
∴当t=
| 12 |
| 5 |
点评:此题主要考查了一元二次方程的应用以及相似三角形的判定与性质、三角形面积求法等知识,此题涉及知识较多,难度不大,关键是要对知识的熟练应用.

练习册系列答案
相关题目
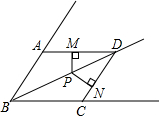 如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.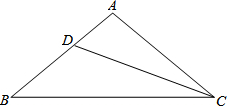 如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.
如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.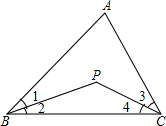 如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为
如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为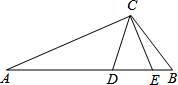 如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.
如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.