题目内容
【题目】如图，二次函数
的图象过原点，与x轴的另一个交点为
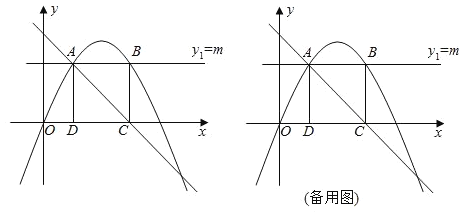
（1）求该二次函数的解析式；
（2）在x轴上方作x轴的平行线
，交二次函数图象于A、B两点，过A、B两点分别作x轴的垂线，垂足分别为点D、点C．当矩形ABCD为正方形时，求m的值；
（3）在（2）的条件下，动点P从点A出发沿射线AB以每秒1个单位长度匀速运动，同时动点Q以相同的速度从点A出发沿线段AD匀速运动，到达点D时立即原速返回，当动点Q返回到点A时，P、Q两点同时停止运动，设运动时间为t秒（
）．过点P向x轴作垂线，交抛物线于点E，交直线AC于点F，问：以A、E、F、Q四点为顶点构成的四边形能否是平行四边形．若能，请求出t的值；若不能，请说明理由．
【答案】（1）
；（2）当矩形ABCD为正方形时，m的值为4；（3）以A、E、F、Q四点为顶点构成的四边形能为平行四边形，t的值为4或6.
【解析】
（1）根据点的坐标，利用待定系数法即可求出二次函数的解析式；
（2）利用二次函数图象上点的坐标特征求出点A，B的坐标，进而可得出点C，D的坐标，再利用正方形的性质可得出关于m的方程，解之即可得出结论；
（3）由（2）可得出点A，B，C，D的坐标，根据点A，C的坐标，利用待定系数法可求出直线AC的解析式，利用二次函数图象上点的坐标特征及一次函数图象上点的坐标特征可求出点E，F的坐标，由
且以A、E、F、Q四点为顶点的四边形为平行四边形可得出
，分
，
，
三种情况找出AQ，EF的长，由可得出关于t的一元二次方程，解之取其合适的值即可得出结论．
（1）将
，
代入
，得：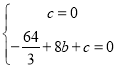
，
解得
，
∴该二次函数的解析式为
．
（2）当
时，
，
解得：
，
，
∴点a的坐标为（
，m），点b的坐标为（
，m），
∴点d的坐标为（，0），点c的坐标为（，0）．
∵矩形abcd为正方形，
∴
，
解得：
，（舍去），
．
∴当矩形ABCD为正方形时，m的值为4．
（3）以A、E、F、Q四点为顶点构成的四边形能为平行四边形．
由（2）可知：点A的坐标为
，点B的坐标为
，点C的坐标为
，点D的坐标为
．
设直线AC的解析式为
，
将
，
代入
，
得
，
解得
，
∴直线ac的解析式为
．
当
时，
，
∴点E的坐标为（
，
），点F的坐标为（，
-t+4）．
∵以A、E、F、Q四点为顶点构成的四边形为平行四边形，且
，
∴，分三种情况考虑：
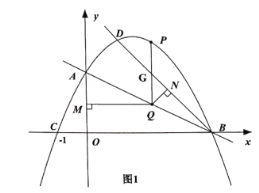
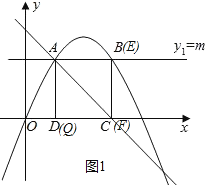
①当时，如图1所示，
，EF=
，
∴
，解得：
（舍去），
；
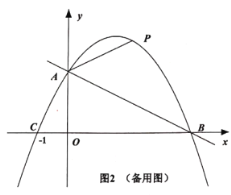
②当时，如图2所示，
，EF=，
∴
，
解得：
（舍去），
；
,, EF=
，
，
解得
（舍去），
（舍去）
综上所述，当以A、E、F、Q四点为顶点构成的四边形为平行四边形时，t的值为4或6
