题目内容
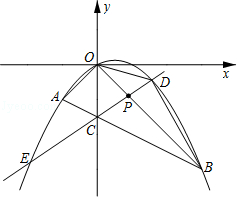
【题目】如图，一次函数
的图像与坐标轴交于A、B两点，点C的坐标为
，二次函数
的图像经过A、B、C三点．
（1）求二次函数的解析式
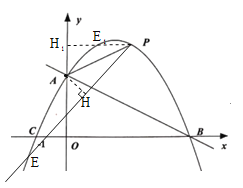
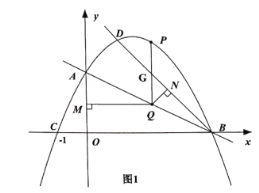
（2）如图1，已知点
在抛物线上，作射线BD，点Q为线段AB上一点，过点Q作
轴于点M，作
于点N，过Q作
轴交抛物线于点P，当QM与QN的积最大时，求点P的坐标；
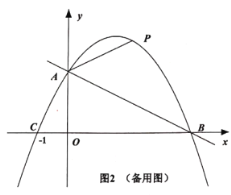
（3）在（2）的条件下，连接AP，若点E为抛物线上一点，且满足
，求点E的坐标．
【答案】（1）
；（2）
；（3）
或
【解析】
（1）求出A、B的坐标，设二次函数解析式为
，把A（0，2）代入即可得出结论；
（2）先求出D的坐标和直线BD的解析式，过D作DT⊥x轴于T，可求得∠DBO=45°．设Q（m，
m+2），则G（m，-m+4），MQ=m．设∠ABO=α，则∠NBQ=45°－α，∠MQB=180°－α．证明ΔGQN为等腰直角三角形，表示出NQ，MQNQ，利用二次函数的性质解答即可；
（3）如图，过A作AH⊥PE于点H，解Rt△APH，得到AH=1，PH=2．设H（m，n），利用两点间距离公式可求出H的坐标，进而求出点E的坐标．
（1）在
中，令x=0，得y=2，∴A（0，2）；
令y=0，得
，解得：x=4，∴B（4，0）．
设二次函数解析式为，
将A（0，2）代入得：
解得：
，
∴．
（2）∵点D（1，n）在抛物线上，∴n=
=3，
∴D（1，3）．
设直线BD的解析式为y=kx+b，则
，
解得：
，
∴直线BD的解析式为：y=-x+4．
过D作DT⊥x轴于T，则OT=1，DT=3．
∵OB=4，∴BT=OB-OT=4-1=3，
∴DT=BT，
∴∠DBO=45°．
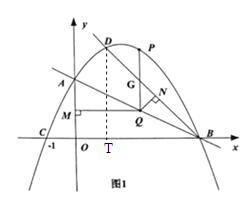
设Q（m，m+2），则G（m，-m+4），MQ=m．
设∠ABO=α，则∠NBQ=45°－α
∠MQB=180°－α．
又∵∠PQM=90°，∠NQB=90°－（45°－α）=45°+α，
∴∠GQN=360°－90°－（180°－α）－（45°+α）=45°，
∴ΔGQN为等腰直角三角形，
∴NQ=
，
∴MQNQ=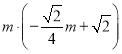
．
当m=2时，QMQN最大，此时P（2，3）．
（3）如图，过A作AH⊥PE于点H，其中，∠APE=∠ABO．
又A（0，2），P（2，3），
，
∴
，
∴PH=2AH．
∵AP=
，
，
∴
，
∴AH=1，PH=2．
设H（m，n），
则
，
，
解得：
；
，
∴
，
．
①易求直线PH的解析式为
：
令
解得：
（舍）
∴
；
②易求直线PH1的解析式为
：
．
令
，
解得：
，
∴
．
综上所述：符合题意的E点坐标为或．
