题目内容
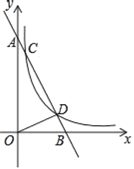
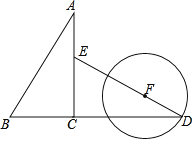
【题目】如图,Rt△ABC中,∠ACB=90°,BC=3,tanA=![]() ,将Rt△ABC绕点C顺时针旋转90°得到△DEC,点F是DE上一动点,以点F为圆心,FD为半径作⊙F,当FD=_____时,⊙F与Rt△ABC的边相切.
,将Rt△ABC绕点C顺时针旋转90°得到△DEC,点F是DE上一动点,以点F为圆心,FD为半径作⊙F,当FD=_____时,⊙F与Rt△ABC的边相切.
【答案】![]() 或
或![]()
【解析】
如图1,当⊙F与Rt△ABC的边AC相切时,切点为H,连接FH,则HF⊥AC,解直角三角形得到AC=4,AB=5,根据旋转的性质得到∠DCE=∠ACB=90°,DE=AB=5,CD=AC=4,根据相似三角形的性质得到DF=![]() ;如图2,当⊙F与Rt△ABC的边AC相切时,延长DE交AB于H,推出点H为切点,DH为⊙F的直径,根据相似三角形的性质即可得到结论.
;如图2,当⊙F与Rt△ABC的边AC相切时,延长DE交AB于H,推出点H为切点,DH为⊙F的直径,根据相似三角形的性质即可得到结论.
如图1,当⊙F与Rt△ABC的边AC相切时,切点为H,
连接FH,则HF⊥AC,

∴DF=HF,
∵Rt△ABC中,∠ACB=90°,BC=3,tanA=![]() =
=![]() ,
,
∴AC=4,AB=5,
将Rt△ABC绕点C顺时针旋转90°得到△DEC,
∴∠DCE=∠ACB=90°,DE=AB=5,CD=AC=4,
∵FH⊥AC,CD⊥AC,
∴FH∥CD,
∴△EFH∽△EDC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:DF=![]() ;
;
如图2,当⊙F与Rt△ABC的边AC相切时,延长DE交AB于H,

∵∠A=∠D,∠AEH=∠DEC
∴∠AHE=90°,
∴点H为切点,DH为⊙F的直径,
∴△DEC∽△DBH,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴DH=![]() ,
,
∴DF=![]() ,
,
综上所述,当FD=![]() 或
或![]() 时,⊙F与Rt△ABC的边相切,
时,⊙F与Rt△ABC的边相切,
故答案为:![]() 或
或![]() .
.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目