题目内容
【题目】阅读下列两则材料,回答问题,
材料一:定义直线y=ax+b与直线y=bx+a互为“互助直线”,例如,直线y=x+4与直y=4x+1互为“互助直线“
材料二:对于平面直角坐标系中的任意两点P1(x1,y1)、P2(x2,y2),P1、P2两点间的直角距离d(P1,P2)=|x1﹣x2|+|y1﹣y2|.例如:Q1(﹣3,1)、Q2(2,4)两点间的直角距离为d(Q1,Q2)=|﹣3﹣2|+|1﹣4|=8
设P0(x0,y0)为一个定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离.
(1)计算S(﹣1,6),T(﹣2,3)两点间的直角距离d(S,T)= ,直线y=2x+3上的一点H(a,b)又是它的“互助直线”上的点,求点H的坐标.
(2)对于直线y=ax+b上的任意一点M(m,n),都有点N(3m,2m﹣3n)在它的“互助直线”上,试求点L(5,﹣![]() )到直线y=ax+b的直角距离.
)到直线y=ax+b的直角距离.
【答案】(1)4;(2)5.
【解析】
(1)根据题中所给出的两点的直角距离公式即可得出结论;求两条直线的交点即可求H点的坐标;
(2)先表示直线y=ax+b的“互助直线”,并将点M和N分别代入可得方程组,得:(3b+3a﹣2)m=﹣a﹣3b,对于任意一点M(m,n)等式均成立,求出a,b的值,再根据题意得出关于x的式子,再由绝对值的几何意义即可得出结论.
解:(1)∵S(﹣1,6)、T(﹣2,3)则S、T两点的直角距离为d(S,T)=|﹣1﹣(﹣2)|+|6﹣3|=4,
∴S(﹣1,6)、T(﹣2,3)两点间的直角距离d(S,T)=4.
直线y=2x+3的“互助直线”是y=3x+2,由题意知H是它们的交点,则有:
![]() ,解得,
,解得,![]() ,
,
∴点H的坐标为:H(1,5).
故答案为:4.
(2)∵点M(m,n)是直线y=ax+b上的任意一点,
∴am+b=n①,
∵点N(3m,2m﹣3n)是直线y=ax+b的“互助直线”上的一点,
即N(3m,2m﹣3n)在直线y=bx+a上
∴3bm+a=2m﹣3n②,
将①代入②得,
3bm+a=2m﹣3(am+b),
整理得:3bm+3am﹣2m=﹣a﹣3b,
∴(3b+3a﹣2)m=﹣a﹣3b,
∵对于任意一点M(m,n)等式均成立,
∴![]() ,
,
解得 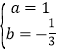 ,
,
∴y=x-![]() .
.
∵Q(x,y)是直线y=x-![]() 上的动点,定点L(5,﹣
上的动点,定点L(5,﹣![]() )
)
∴Q(x,x﹣![]() ),
),
∴d(L,Q)=|5﹣x|+|﹣![]() ﹣(x﹣
﹣(x﹣![]() )|=|5﹣x|+|﹣x|,
)|=|5﹣x|+|﹣x|,
∵当0≤x≤5时,代数式|5﹣x|+|﹣x|有最小值5,
∴点L(5,﹣![]() )到直线y=x-
)到直线y=x-![]() 的直角距离是5.
的直角距离是5.

 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案