Question

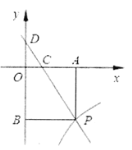
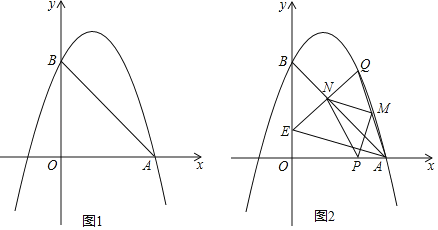
【题目】如图，抛物线y＝﹣x2+bx+c与x轴正半轴交于A点，与y轴正半轴交于B，直线AB的解析式为y＝﹣x+3．

（1）求抛物线解析式；

（2）P为线段OA上一点（不与O、A重合），过P作PQ⊥x轴交抛物线于Q，连接AQ，M为AQ中点，连接PM，过M作MN⊥PM交直线AB于N，若点P的横坐标为t，点N的横坐标为n，求n与t的函数关系式；

（3）在（2）的条件下，连接QN并延长交y轴于E，连接AE，求t为何值时，MN∥AE．

Answer 1

【答案】（1）y＝﹣x2+2x+3；（2）Nx＝3﹣＝（0＜t＜3）；（3）2．

【解析】

（1）求出A、B两点坐标，利用待定系数法即可解决问题；

（2）如图1中，过点M作MG⊥x轴于G，NH⊥GM，于H．首先证明N、P、A三点在以M为圆心MA为半径的⊙M上，再根据△NMH≌△MPG，得到NH＝MG，HM＝PG，即可解决问题；

（3）如图2中，MN∥AE，QM＝MA，得EN＝QN，利用中点坐标公式，列出方程即可解决问题．

解：（1）∵直线AB的解析式为y＝﹣x+3，

∴A（3，0），B（0，3），

∵抛物线y＝﹣x2+bx+c经过A点，B点，

∴，解得，

∴抛物线解析式为y＝﹣x2+2x+3；

（2）如图1中，过点M作MG⊥x轴于G，NH⊥GM，于H，

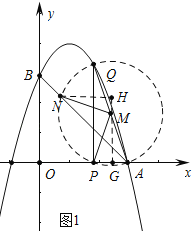
∵OA＝OB，∠AOB＝90°，

∴∠PAN＝45°，

∵∠NMP＝90°，

∴∠PAN＝∠NMP，

∴N、P、A三点在以M为圆心MA为半径的⊙M上，

∴MN＝MP，

∵∠NHM＝∠PGM＝∠NMP＝90°，

∴∠NMH+∠PMG＝90°，∠PMG+∠MPG＝90°，

∴∠NMH＝∠MPG，

∴△NMH≌△MPG，

∴NH＝MG，HM＝PG，

∵P（t，0），

∴Q（t，﹣t2+2t+3），M（，），

∴PG＝MH＝﹣t＝，HG＝+＝，

∴Ny＝，

∵点N在直线AB上，

∴Ny＝﹣Nx+3，

∴Nx＝3﹣＝（0＜t＜3）；

（3）如图2中，

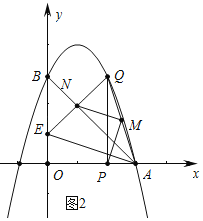
∵MN∥AE，QM＝MA，

∴EN＝QN，

∴＝，

∴t2﹣2t＝0，

解得t＝2或0（舍弃），

∴t＝2时，MN∥AE．