��Ŀ����
����Ŀ����ͼ����![]() ������
������![]() ��ƽ����
��ƽ����![]() ��
��
��1�������dzߵ�ֱ�Ƕ�������![]() ������һ��P�ϣ�ʹ���dzߵ�����ֱ�DZ���
������һ��P�ϣ�ʹ���dzߵ�����ֱ�DZ���![]() �����߷ֱ�ֱ������ΪE��F����ͼ1������
�����߷ֱ�ֱ������ΪE��F����ͼ1������![]() �� ��
�� ��![]() ��ѡ�����������
��ѡ�����������

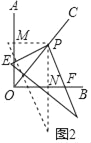
��2�������dz����ŵ�P��ת����ͼ2����![]() ��
��![]() ������Բ���
������Բ���![]() ��
��![]() �Ĵ�С��ϵ����˵�����ɣ�
�Ĵ�С��ϵ����˵�����ɣ�
��չ����1���ڣ�2�������£�����P��ֱ��![]() ���ֱ�
���ֱ�![]() ��
��![]() �ڵ�G��H����ͼ3
�ڵ�G��H����ͼ3
��ͼ��ȫ���������ж��ٶԣ������Ӹ����ߣ�
�ڲ���![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ����֤����IJ��룮
֮��Ĺ�ϵ����֤����IJ��룮
��չ����2��
��![]() ������
������![]() ��ƽ����
��ƽ����![]() ����
����![]() ����ȡһ��P����
����ȡһ��P����![]() ��
��![]() �����߷ֱ���
�����߷ֱ���![]() ��
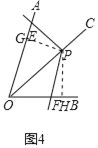
��![]() �ཻ��E��F���㣨��ͼ4����
�ཻ��E��F���㣨��ͼ4����![]() ��
��![]() �������˵�����ɣ�
�������˵�����ɣ�
���𰸡���1��������2��![]() �����ɼ���������չ����1����ȫ����������3�ԣ���
�����ɼ���������չ����1����ȫ����������3�ԣ���![]() �����ɼ���������չ����2��
�����ɼ���������չ����2��![]() �����ɼ�������
�����ɼ�������
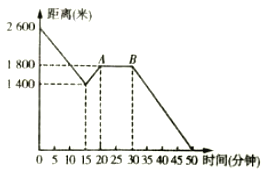
��������
��1�����ݽ�ƽ���ߵ����ʶ���֤����
��2��֤����MPE�ա�NPF������ȫ�������ε�����֤�����ۣ�
��չ����1���ٸ��ݵ���ֱ�������ε����ʵõ�OP=PG=PH��֤����GPE�ա�OPF��ASA������EPO�ա�FPH����GPO�ա�OPH���õ��𰸣�
�ڸ��ݹ��ɶ�����ȫ�������ε����ʽ��
��չ����2����PG��OA��G��PH��OB��H��֤����PGE�ա�PHF������ȫ�������ε�����֤�����ۣ�
��1����![]() ƽ��
ƽ��![]() ��
��
��![]() ��
��
�ʴ�Ϊ������
��2��![]() ��
��
�������£���![]() ��
��
��![]() ��
��
�ɣ�1���ã�![]() ��
��
��![]() ��
��![]() ��
�У�
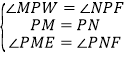 ��
��
��![]() ��
��
��![]() ��
��
��չ����1���١�![]() ƽ��
ƽ��![]() ��
��
��![]() ��
��
��GH��OC��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
�У�
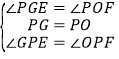 ��
��
��![]() ��
��
ͬ����![]() ��
��
�ʴ�Ϊ��3��
��![]() ��
��
�������£���![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��չ����2��![]() ��
��
���ɣ���![]() ��G��
��G��![]() ��H��
��H��
��![]() ƽ��
ƽ��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
�У�
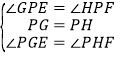 ��
��
��![]() ��
��
��![]() ��
��