题目内容
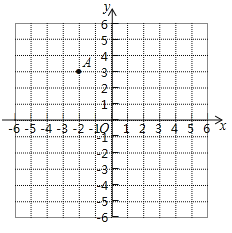
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|2a﹣b+8|+(a+b﹣2)2=0.

(1)求a、b的值;
(2)如图1,点G在y轴上,三角形COG的面积是三角形ABC的面积的![]() ,求出点G的坐标;
,求出点G的坐标;
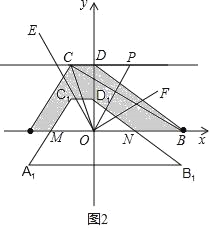
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一个动点,连接OP、AC、DB,OE平分∠AOP,OF⊥CE,若∠OPD+k∠DOF=k(∠FOP+∠AOE),现将四边形ABDC向下平移![]() k个单位得到四边形A1B1D1C1,已知AM+BN =
k个单位得到四边形A1B1D1C1,已知AM+BN =![]() k,求图中阴影部分的面积.
k,求图中阴影部分的面积.
【答案】(1)a=﹣2,b=4;(2)G(0,6)或(0,﹣6);(3)S阴=![]() .
.
【解析】
(1)利用非负数的性质即可解决问题;
(2)过点C作CT⊥AB于T.根据面积关系求出OG的长即可解决问题;
(3)设∠AOE=x,则∠AOP=2∠AOE=2x,∠POB=180°-2x,由CD∥AB,推出∠OPD=∠POB=180°-2x,由∠DOF=∠AOE,推出∠OPD+k∠DOF=k∠FOP+k∠AOE,推出∠OPD=k∠FOP,可得180°-2x=k(90°-x),推出k=2,即可解决问题.
(1)∵|2a﹣b+8|+(a+b﹣2)2=0,
又∵|2a﹣b+8|≥0,(a+b﹣2)2≥0,
∴![]() ,
,
解得![]() ,
,
∴a=﹣2,b=4.
(2)如图1中,过点C作CT⊥AB于T.
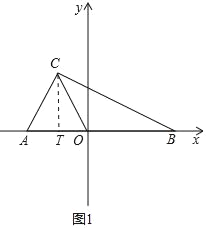
∵C(﹣1,2),
∴CT=2,
∵S△ABC=![]() ×6×2=6,
×6×2=6,
∴S△OCG=![]() ×1×OG=3,
×1×OG=3,
∴OG=6,
∴G(0,6)或(0,﹣6).
(3)如图2中,
设∠AOE=x,
∵OE平分∠AOP,
∴∠AOP=2∠AOE=2x,
∵∠AOB=180°,
∴∠POB=180°﹣2x,
∵CD⊥y轴,AB⊥y轴,
∴∠CDO=∠DOB=90°,
∴CD∥AB,
∴∠OPD=∠POB=180°﹣2x,
∵OF⊥OE,
∴∠FOP=90°﹣x,
∵∠AOD=90°,
∴∠AOE+∠EOD=∠DOF+∠EOD=90°,
∴∠DOF=∠AOE,
∴∠OPD+k∠DOF=k∠FOP+k∠AOE,
∴∠OPD=k∠FOP,
∴180°﹣2x=k(90°﹣x),
∴k=2,
∴![]() ,
,
∴AM+BN=![]() ,
,
∴S阴=S四边形MNB1A1=![]() .
.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案