题目内容
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
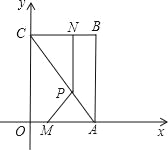
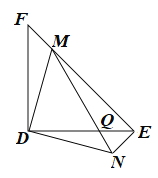
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
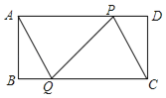
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.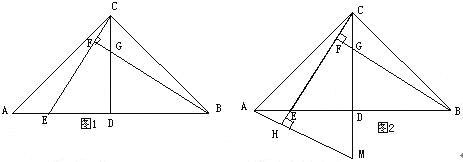
【答案】解:(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,又BF⊥CE,
∴∠CBG+∠BCF=90°,又∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
∴△AEC≌△CGB,
∴AE=CG,
(2)BE=CM,
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵AC=BC,∠ACM=∠CBE=45°,
∴△BCE≌△CAM,
∴BE=CM.
【解析】
⑴证明:设∠ACE=∠1,因为直线BF垂直于CE,交CE于点F,所以∠CFB=90°,
所以∠ECB+∠CBF=90°.
又因为∠1+∠ECB=90°,所以∠1=∠CBF .
因为AC="BC," ∠ACB=90°,所以∠A=∠CBA=45°.
又因为点D是AB的中点,所以∠DCB=45°.
因为∠1=∠CBF,∠DCB=∠A,AC=BC,所以△CAE≌△BCG,所以AE=CG.
(2)解:CM=BE.证明如下:因为∠ACB=90°,所以∠ACH +∠BCF=90°.
因为 CH⊥AM,即∠CHA=90°,所以 ∠ACH +∠CAH=90°,所以∠BCF=∠CAH.
因为 CD为等腰直角三角形斜边上的中线,所以 CD=AD.所以∠ACD=45°.
在△CAM与△BCE中,CA=BC,∠CAH =∠BCF, ∠ACM =∠CBE,
所以 △CAM ≌△BCE,所以CM=BE.

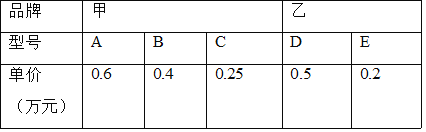
【题目】光明中学七年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
项目选择情况统计图训练后篮球定时定点投篮测试进球数统计表
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)选择长跑训练的人数占全班人数的百分比是_____%,该班共有同学_____人;
(2)求训练后篮球定时定点投篮人均进球数;
(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%.请求出参加训练之前的人均进球数.