Question

【题目】菱形 ABCD 的对角线 AC=4，BD=2，以 AC 为边作正方形 ACEF，则 BF 的长为_____．

Answer 1

【答案】或

【解析】

作出图形，根据菱形的对角线互相垂直平分求出AO、BO，然后分正方形在AC的两边两种情况补成以BF为斜边的Rt△BKF，然后求出BK、FK，再利用勾股定理列式计算即可得解．

解∵AC=4，BD=2，

∴AO=2，BO=1，

如图1，正方形ACEF在AC的左边时，过点B作BK⊥AF交FA于K，

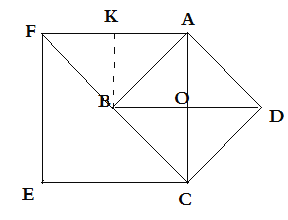
∴BK=AO=2，FK=AF-AK=3，

在Rt△BFK中，BF==，

如图，正方形ACEF在AC的右边时，过点B作BK⊥AF交FA的延长线于K

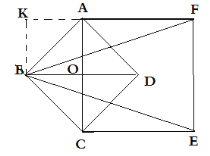
∴BK=AO=2，FK=AF+AK=5，

在Rt△BFK中，BF==，

故答案为：或.