��Ŀ����
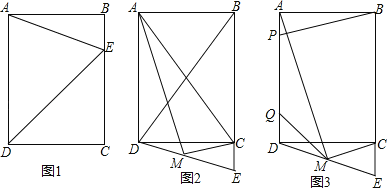
����Ŀ����֪����ͼ���ھ���ABCD�У�AB��6��BC��8��EΪֱ��BC��һ�㣮
��1����ͼ1����E���߶�BC�ϣ���DE��ADʱ����BE�ij���
��2����ͼ2����EΪBC�ӳ�������һ�㣬��BD��BE������DE��MΪED���е㣬����AM��CM����֤��AM��CM��
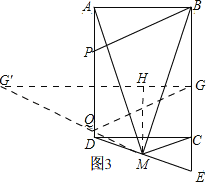
��3����ͼ3���ڣ�2�������£�P��QΪAD���ϵ��������㣬��PQ��5������PB��MQ��BM�����ı���PBMQ���ܳ�����Сֵ��
���𰸡���1��BE=8��2![]() ����2��֤������������3��
����2��֤������������3��![]() +5+3
+5+3![]() ��
��
��������
��1�������DE��AD��4������ù��ɶ������ɵó����ۣ�
��2�����жϳ���BMD��90�������жϳ���ADM�ա�BCM�ó���AMD����BMC�����ɵó����ۣ�
��3������BM��PQ�Ƕ�ֵ��ֻҪBP+QM��С�����öԳ�ȷ����MG'����BP+QM����Сֵ��������ù��ɶ������ɵó����ۣ�
�⣺��1����ͼ1�У����ı���ABCD�Ǿ��Σ�
���C��90����CD��AB��6��AD��BC��8��
��DE��AD��8��
��Rt��CDE��CE��![]() ��
��
��BE��BC��CE��8��2![]() ��
��
��2����ͼ2������BM��
����M��DE���е㣬
��DM��EM��
��BD��BE��
��BM��DE��
���BMD��90����
����M��Rt��CDE��б�ߵ��е㣬
��DM��CM��
���CDM����DCM��
���ADM����BCM
����ADM����BCM��
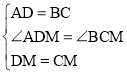 ��
��
���ADM�ա�BCM��SAS����
���AMD����BMC��
���AMC����AMB+��BMC����AMB+��AMD����BMD��90����
��AM��CM��
��3����ͼ3�У�����Q��QG��BP��BC��G������G����AD�ĶԳƵ�G'������QG'������G'��Q��M��ͬһ������ʱ��QM+BP��С����PQ��BM�Ƕ�ֵ��
����ʱ���ı���PBMQ�ܳ���С��
��QG��PB��PQ��BG��
���ı���BPQG��ƽ���ı��Σ�
��QG��BP��BG��PQ��5��
��CG��3����ͼ2����Rt��BCD�У�CD��6��BC��8��
��BD��10��
��BE��10��
��BG��BE��BG��5��CE��BE��BC��2��
��HM��1+3��4��HG��![]() CD��3��
CD��3��
��Rt��MHG'��HG'��6+3��9��HM��4��
��MG'��![]() ��
��
��Rt��CDE��DE��![]() ��
��
��ME��![]() ��
��
��Rt��BME��BM��![]() ��3
��3![]() ��
��
���ı���PBMQ�ܳ���СֵΪBP+PQ+MQ+BM��QG+PQ+QM+BM��MG'+PQ+PM��![]() +5+3
+5+3![]() ��
��