题目内容
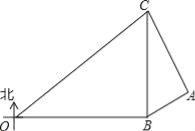
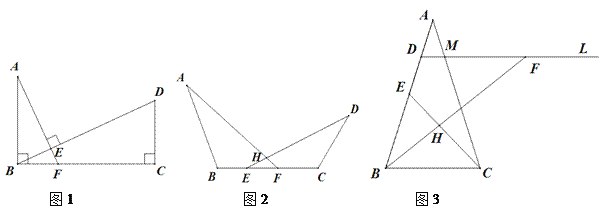
【题目】(1)【特殊发现】如图1,AB⊥BC于B,CD⊥BC于C,连接BD,过A作AF⊥BD,交BD于E,交BC于F,若BF=1,BC=3,则AB·CD= ;
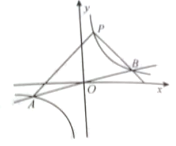
(2)【类比探究】如图2,在线段BC上存在点E,F,连接AF,DE交于点H,若∠ABC=∠AHD=∠ECD,求证:AB·CD=BF·CE;
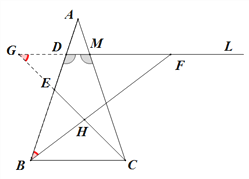
(3)【解决问题】如图3,在等腰△ABC中,AB=AC=4,E为AB中点,D为AE中点,过点D作直线DM∥BC,在直线DM上取一点F,连接BF交CE于点H,使∠FHC=∠ABC,问:DF·BC是否为定值?若是,请求出,若不是,请说明理由.
【答案】(1)3;(2)详见解析;(3)是,DF·BC=12,理由详见解析.
【解析】试题分析:(1)先由余角的性质得到∠A=∠CBD,从而△ABF∽△BCD,再根据相似三角形的性质列比例式求解;(2)由∠ABC=∠AHD=∠ECD,得到∠AFB=∠EDC,从而△ABF∽△ECD,
再根据相似三角形的性质列比例式求解;(3)法一,在DA的延长线上取一点N,使∠DNF=∠ABC,然后由△FDN∽△ABC和△NFB∽△BEC,得到![]() 和
和![]() ,然后整理即可得到结论;法二,取BC的中点K,连接EK,由E为AB中点,然后由△FDB∽△EKC,得到
,然后整理即可得到结论;法二,取BC的中点K,连接EK,由E为AB中点,然后由△FDB∽△EKC,得到![]() ,然后结合法一整理即可得到结论;法三,延长FD,CE交于点G,由法一得:∠ADM=∠AMD,∠ABF=∠ECB,然后由△GMC∽△BDF和△GED∽△CEB,得到
,然后结合法一整理即可得到结论;法三,延长FD,CE交于点G,由法一得:∠ADM=∠AMD,∠ABF=∠ECB,然后由△GMC∽△BDF和△GED∽△CEB,得到![]() 和
和![]() ,然后整理即可得到结论;
,然后整理即可得到结论;
解: (1) ∵AB⊥BC,AF⊥BD,
∴∠A+∠AFB=90°, ∠CBD+∠AFB=90°,
∴∠A=∠CBD,
又∵∠ABF=∠C,
∴△ABF∽△BCD,
![]() ,
,
∴ AB·CD=BC·BF=3.
(2)容易由∠ABC=∠AHD=∠ECD,得到∠AFB=∠EDC,
从而△ABF∽△ECD,
那么AB·CD=BF·CE;
(3)法一:(模型法)解:是,DF·BC=12,
理由如下:
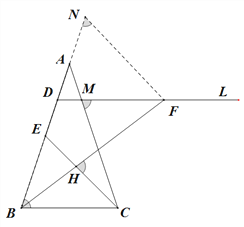
如图,在DA的延长线上取一点N,使∠DNF=∠ABC,
由AB=AC,DM∥BC,可得:∠ADM=∠AMD=∠ABC=∠ACB∠FMC=∠DNF,
∴△FDN∽△ABC,且DF=NF,∴![]() 即NF·BC=ND·AB,
即NF·BC=ND·AB,
又由∠ABC=∠FHC,得∠ABF+∠FBC=∠FBC+∠ECB,
∴∠ABF=∠ECB,∴△NFB∽△BEC,
∴![]() 即NF·BC=NB·BE,
即NF·BC=NB·BE,
∴NB·BE=ND·AB,依题意得:AD=DE=1,BE=2,
∴NB·2=ND·4,∴NB=2ND,∴ND=BD=3,
∴NB=6,∴NF·BC=6×2=12即DF·BC=12。
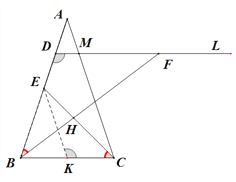
法二:(平行法)取BC的中点K,连接EK,由E为AB中点,
∴EK![]()
![]() AC,得∠ADM=∠ABC=∠EKB,
AC,得∠ADM=∠ABC=∠EKB,
∴∠BDF=∠EKC,再由法一可知:∠DBF=∠ECB,
∴△FDB∽△EKC,∴![]() ,即DF·CK=EK·DB,
,即DF·CK=EK·DB,
由法一得:DB=3,EK=BE=2,CK=![]() BC,
BC,
∴DF·![]() BC=2×3,∴DF·BC=12。
BC=2×3,∴DF·BC=12。
法三:延长FD,CE交于点G,由法一得:∠ADM=∠AMD,∠ABF=∠ECB,
∴∠BDM=∠CMD,又∵DF∥BC,∴∠G=∠ECB,∴∠G=∠ABF,
∴△GMC∽△BDF,∴![]() ,∴DF·GM=MC·DB=3×3=9,
,∴DF·GM=MC·DB=3×3=9,
又∵GD∥BC,DE=1,BE=2,
∴△GED∽△CEB,∴![]() ,
,
同理![]() ,∴GM=GD+DM=
,∴GM=GD+DM=![]() BC+
BC+![]() BC=
BC=![]() BC,
BC,
∴DF·![]() BC=9,∴DF·BC=12。
BC=9,∴DF·BC=12。