Question

【题目】（1）已知∠AOB＝25°42′，则∠AOB的余角为　 　，∠AOB的补角为　 　；

（2）已知∠AOB＝α，∠BOC＝β，OM平分∠AOB，ON平分∠BOC，用含α，β的代数式表示∠MON的大小；

（3）如图，若线段OA与OB分别为同一钟表上某一时刻的时针与分针，且∠AOB＝25°，则经过多少时间后，△AOB的面积第一次达到最大值．

Answer 1

【答案】（1）64°18′，154°18′；（2）∠MON＝；（3）分

【解析】

（1）依据余角和补角的定义即可求出∠AOB的余角和补角；
（2）依据角平分线的定义表示出∠AOM=∠BOM=∠AOB=α，∠CON=∠BON=∠COB=β，最后再依据∠MON与这些角的关系求解即可；（3）当OA⊥OB时面积最大，此时∠AOB＝90°，根据角的和差关系可得求出三角形OBC面积第一次达到最大的时间.

解：（1）∵∠AOB＝25°42'，

∴∠AOB的余角＝90°﹣25°42'＝64°18′，

∠AOB的补角＝180°﹣25°42'＝154°18′；

故答案为：64°18′，154°18′；

（2）

①如图1：

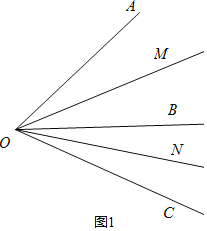
∵∠AOB＝α，∠BOC＝β

∴∠AOC＝∠AOB+∠BOC＝90°+30°＝120°

∵OM平分∠AOB，ON平分∠BOC，

∴∠AOM＝∠BOM＝∠AOB＝α，∠CON＝∠BON＝∠COB＝β，

∴∠MON＝∠BOM+∠CON＝；

②如图2，

∠MON＝∠BOM﹣∠BON＝；

③如图3，

∠MON＝∠BON﹣∠BOM＝．

∴∠MON为或或．

（3）当OA⊥OB时，△AOB的面积第一次达到最大值，此时∠AOB＝90°，

设经过x分钟后，△AOB的面积第一次达到最大值，

根据题意得：6x+25﹣×30＝90，

解得x＝．