题目内容
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.

(1)求证:AM是⊙O的切线;
(2)若∠D = 60°,AD = 2,射线CO与AM交于N点,请写出求ON长的思路.
【答案】证明见解析
【解析】试题分析:(1)根据垂径定理得到AB垂直平分CD,根据线段垂直平分线的性质得到AC=AD,得到∠BAD=![]() ∠CAD,由AM是△ACD的外角∠DAF的平分线,得到∠DAM=
∠CAD,由AM是△ACD的外角∠DAF的平分线,得到∠DAM=![]() ∠FAD,再由∠BAD与∠FAD互补,得出∠BAM=90°,根据切线的判定即可得到结论;
∠FAD,再由∠BAD与∠FAD互补,得出∠BAM=90°,根据切线的判定即可得到结论;
(2)根据有一个角是60°的等腰三角形是等边三角形推出△ACD是等边三角形,得到CD=AD=2,再根据等边三角形的性质和三角形的内角和定理求出∠5=∠4=30°,AN=AC=2,利用三角函数解直角三角形即可得到结论.
试题解析:
(1)证明:∵AB⊥CD,AB是⊙O的直径,
∴![]() .
.
∴![]() .
.
∵AM是∠DAF的角平分线,
∴![]() .
.
∵![]() °,
°,
∴![]() °.
°.
∴OA⊥AM.
∴AM是⊙O的切线.
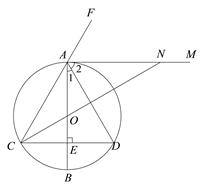
(2)思路:①由AB⊥CD,AB是⊙O的直径,可得AC=AD,∠1=∠3=![]() ∠CAD;
∠CAD;
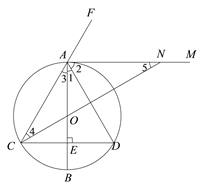
②由∠D=60°,AD=2,可得△ACD为边长为2的等边三角形,∠1=∠3=30°;
③由OA=OC,可得∠4=∠3=30°;
④由∠CAN=∠3+∠BAN=30°+90°=120°,可得∠5=∠4=30°,AN=AC=2;
⑤在Rt△OAN中,根据三角函数即可求出ON的长.

练习册系列答案
相关题目