��Ŀ����
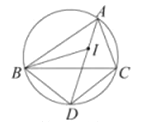
����Ŀ����ij�κ��Ͼ���ѧϰ�ڼ䣬�Ҿ�Ϊȷ����OBC�����ڵİ�ȫ������Dz���Ҿ����ֱ���O��B��C�������OBC�������״���ʾͼ�ϣ�����B�ھ���O����������80���ﴦ������C�ھ���B����������60���ﴦ�����Ҿ�����װ������ͬ��̽���״�״����Ч̽�ⷶΧ�ǰ뾶Ϊr��Բ������ֻ�����ں�ƽ���ϵ�̽�⣩
��1�������Ҿ���Ҫ����OBC���������ä���أ����״����Ч̽��뾶r����Ϊ���ٺ��
��2������һ�ҵн�A�Ӷ����ӽ���OBC������ijһʱ�̾���B���Aλ�ڱ�ƫ��60�������ϣ�ͬʱ����C���Aλ����ƫ��30�������ϣ����ʱ�н�A����OBC�������̾���Ϊ���ٺ��
��3�����н�A����̾����·����20![]() ����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15���ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15���ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
���𰸡���1���״����Ч̽��뾶r����Ϊ50�����2���н�A����OBC�������̾���Ϊ15![]() �����3��B�����ٶ�����Ϊ20����/Сʱ��
�����3��B�����ٶ�����Ϊ20����/Сʱ��
��������
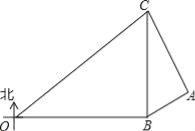
�����������1����RT��OBC�У����ݹ��ɶ������OC��������r��![]() OC���ɴ˵ô𰸣���2����AM��BC��M�������AB�ij�����RT��ABM�����AM�ij����ɵô𰸣���3������B�����ڵ�N�����ص��н�����BM��ȡһ��H��ʹ��HB=HN����MN=x�����г��������x�������BN��AN���ò���ʽ������⣮
OC���ɴ˵ô𰸣���2����AM��BC��M�������AB�ij�����RT��ABM�����AM�ij����ɵô𰸣���3������B�����ڵ�N�����ص��н�����BM��ȡһ��H��ʹ��HB=HN����MN=x�����г��������x�������BN��AN���ò���ʽ������⣮
�����������1����RT��OBC����BO=80��BC=60����OBC=90����
��OC=![]() ��
��
��![]() OC=
OC=![]() ��100=50
��100=50
���״����Ч̽��뾶r����Ϊ50���
��2����AM��BC��M��
�ߡ�ACB=30������CBA=60����
���CAB=90����
��AB=![]() BC=30��
BC=30��
��RT��ABM�У��ߡ�AMB=90����AB=30����BAM=30����
��BM=![]() AB=15��AM=
AB=15��AM=![]() BM=15
BM=15![]() ��
��
����ʱ�н�A����OBC�������̾���Ϊ15![]() ���
���
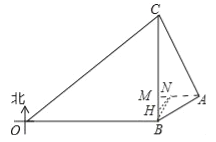
��3������B�����ڵ�N�����ص��н�����BM��ȡһ��H��ʹ��HB=HN����MN=x��
�ߡ�HBN=��HNB=15����
���MHN=��HBN+��HNB=30����
��HN=HB=2x��MH=![]() x��
x��
��BM=15��
��15=![]() x+2x��
x+2x��
x=30��15![]() ��
��
��AN=30![]() ��30��
��30��
BN=![]() ����B�����ٶ�Ϊa����/Сʱ��
����B�����ٶ�Ϊa����/Сʱ��
������![]() ��
��
��a��20��
��B�����ٶ�����Ϊ20����/Сʱ��

����Ŀ��Ϊ�˽�ѧ�������ڼҵ��Ķ���������������20��ѧ��ijһ����Ķ�Сʱ��������ͳ�����£�
�Ķ�ʱ�䣨Сʱ�� | 2 | 2.5 | 3 | 3.5 | 4 |
ѧ������������ | 1 | 2 | 8 | 6 | 3 |
�������20��ѧ���Ķ�Сʱ��������_____��