题目内容
【题目】当k值相同时,我们把正比例函数![]() 与反比例函数
与反比例函数![]() 叫做“关联函数”.
叫做“关联函数”.
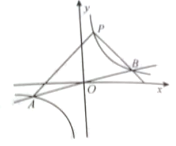
(1)如图,若k>0,这两个函数图象的交点分别为A,B,求点A,B的坐标(用k表示);
(2)若k=1,点P是函数![]() 在第一象限内的图象上的一个动点(点P不与B重合),设点P的坐标为(
在第一象限内的图象上的一个动点(点P不与B重合),设点P的坐标为(![]() ),其中m>0且m≠2.作直线PA,PB分别与x轴交于点C,D,则△PCD是等腰三角形,请说明理由;
),其中m>0且m≠2.作直线PA,PB分别与x轴交于点C,D,则△PCD是等腰三角形,请说明理由;
(3)在(2)的基础上,是否存在点P使△PCD为直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)点A坐标为(-k,-1),点B坐标(k,1);(2)△PCD是等腰三角形;,理由见解析;(3)不存在,理由见解析.
【解析】
(1)联立两个函数解析式即可;
(2)先求出点C和点D的坐标,然后根据两点距离公式得到PC=PD即可;
(3)过点P作PH⊥CD于H,根据等腰直角三角形的性质可得CD=2PH,可求m的值;然后再点P不与B重合即可解答.
解:(1)∵两个函数图象的交点分别为点A和点B,
∴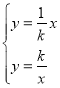 ,解得:
,解得:![]() 或
或![]()
∴点A坐标为(-k,-1),点B坐标(k,1);
(2)△PCD是等腰三角形,理由如下:
∵k=1
∴点A和点B的坐标为(-1,-1)和(1,1),
设点P的坐标为(m,![]() )
)
∴直线PA解析式为:![]()
∵当y=0时,x=m-1,
∴点C的坐标为(m-1,0)
同理可求直线PB解析式为:![]()
∵当y=0时,x=m+1,
∴点D的坐标为(m+1,0)
∴ ,
,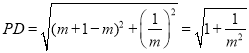
∴PC=PD
∴△PCD是等腰三角形;
(3)如图:过点P作PH⊥CD于H
∵△PCD直角三角形,PH⊥CD,
∴CD=2PH,
∴m+1-(m-1)=2×![]() ,解得m=1
,解得m=1
∴点P的坐标为(1,1),
∵点B(1,1)与点函数![]() 在第一象限内的图象上的一个动点P不重合
在第一象限内的图象上的一个动点P不重合
∴不存在点P使△PCD为直角三角形.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目