题目内容
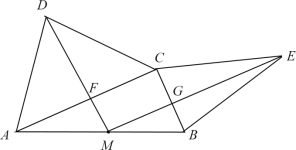
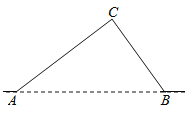
【题目】如图，从
地到
地的公路需经过
地，图中
，
，
，因城市规划的需要，将在
两地之间修建一条笔直的公路.
（Ⅰ）求改直的公路
的长；
（Ⅱ）问公路改直后比原来缩短了多少
？（参考数据：
，
，
，
取
.）（结果保留小数点后一位）.
【答案】（1）改直后的公路
的长为
千米；（Ⅱ）改直后的路程缩短了
千米.
【解析】
（Ⅰ）过点C作CH⊥AB与H，根据AC=30千米，∠CAB=25°，求出CH、AH，根据∠CBA=45°，求出BH，最后根据AB=AH+BH列式计算即可，
（Ⅱ）在
中，根据锐角三角函数求出BC，再根据AC、BC和AB的值，即可得出公路改直后该段路程比原来缩短的路程．
解：（1）过点
作
于点
，
在
中，
，
，
∴
；
；
又在中，∵
，∴
，
∴
.
答：改直后的公路的长为千米；
（Ⅱ）在中，
，
∴
，
∴
（千米）
答：改直后的路程缩短了千米.
练习册系列答案
备战中考寒假系列答案
相关题目
【题目】某专卖店准备购进甲、乙两种运动鞋，其进价和售价如下表所示。已知用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
运动鞋价格 | 甲 | 乙 |
进价元/双) | m | m-30 |
售价(元/双) | 300 | 200 |
(1)求m的值；
(2)要使购进的甲，乙两种运动鞋共200双的总利润不少于21700元且不超过22300元，问该专卖店有几种进货方案?
(3)在(2)的条件下，专卖店决定对甲种运动鞋每双优惠a(60<a<80)元出售，乙种运动鞋价格不变，那么该专卖店要获得最大利润应如何进货?
