题目内容
【题目】在平面直角坐标系xOy中，函数y1＝
x﹣2的图象与函数y2＝
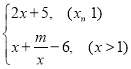的图象在第一象限有一个交点A，且点A的横坐标是6．
（1）求m的值；
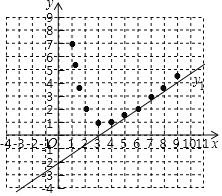
（2）补全表格并以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点，补充画出y2的函数图象；
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 1.2 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y2 | ﹣1 | 1 | 5 | 7 | 5.2 | 3.5 | 2 | 1 | 1 | 2 |
|
|
|
（3）写出函数y2的一条性质： ；
（4）已知函数y1与y2的图象在第一象限有且只有一个交点A，若函数y3＝x+n与y2的函数图象有三个交点，求n的取值范围．
【答案】（1）m＝12；（2）3，
；图见解析；（3）当x≤1时，y2随着x的增大而增大（答案不唯一）；（4）﹣2＜n＜
【解析】
（1）将点A的横坐标代入y1＝
x﹣2可得出点A的坐标，再将A（6，2）代入y2＝x+
﹣6，可得m的值；
（2）根据函数解析式进行计算，即可得到函数值，在直角坐标系内描出相应的点，即可画出y2的函数图象；
（3）依据函数图象的增减性，即可写出函数y2的一条性质；
（4）当n＝﹣2时，函数y3＝x+n与y2的函数图象有两个交点，当函数y3＝x+n的图象经过（1，7）时，函数y3＝x+n与y2的函数图象有两个交点，据此可得n的取值范围．
解：（1）在y1＝x﹣2中，令x＝6，则y＝2，即A（6，2），
代入y＝x+﹣6，可得
2＝6+
﹣6，
解得m＝12；
（2）∵y2＝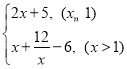
，
∴当x＝﹣1时，y2＝3；
当x＝5时，y2＝；
故表格中应填：3；；
y2的图象如图所示：
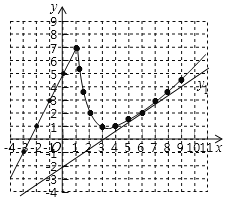
（3）由图可得，函数y2的一条性质：当x≤1时，y2随着x的增大而增大；
故答案为：当x≤1时，y2随着x的增大而增大(答案不唯一)；
（4）函数y1与y2的图象在第一象限有且只有一个交点A，
当n＝﹣2时，函数y3＝x+n与函数y1＝x﹣2的图象重合，
此时函数y3＝x+n与y2的函数图象有两个交点，
当函数y3＝x+n的图象经过（1，7）时，函数y3＝x+n与y2的函数图象有两个交点，
此时，把（1，7）代入y3＝x+n，可得n＝；
∵函数y3＝x+n与y2的函数图象有三个交点，
∴n的取值范围为﹣2＜n＜．
【题目】行驶中的汽车，在刹车后由于惯性的原因，还要继续向前滑行一段距离才能停住，这段距离称为“刹车距离”．为了测定某种型号汽车的刹车性能，对这种汽车的刹车距离进行测试，测得的数据如下表：
刹车时车速(千米/时) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
刹车距离(米) | 0 | 0.1 | 0.3 | 0.6 | 1 | 1.6 | 2.1 |
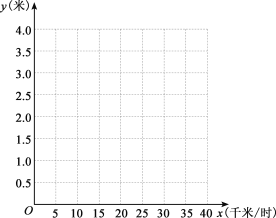
（1）在如图所示的直角坐标系中，以刹车时车速为横坐标，以刹车距离为纵坐标，描出这些数据所表示的点，并用平滑的曲线连结这些点，得到某函数的大致图象；
（2）测量必然存在误差，通过观察图象估计函数的类型，求出一个大致满足这些数据的函数表达式；
（3）一辆该型号汽车在高速公路上发生交通事故，现场测得刹车距离约为40米，已知这条高速公路限速100千米/时，请根据你确定的函数表达式，通过计算判断在事故发生时，汽车是否超速行驶．
