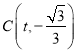题目内容
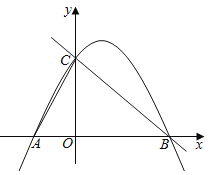
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴是直线x=1.
(1)求抛物线的解析式.
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为15,若存在,求出点F的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+x+4;(2)存在点F使四边形ABFC的面积为15,此时,点F的坐标为(1,
x2+x+4;(2)存在点F使四边形ABFC的面积为15,此时,点F的坐标为(1,![]() )或(3,
)或(3,![]() )
)
【解析】
(1)利用待定系数法求出二次函数解析式;
(2)连接BF、CF、OF,作FG⊥x轴于点G,设点F的坐标为(t,﹣![]() t2+t+4),用t分别表示出S△OBF、S△OCF、S△AOC,根据题意列式计算即可.
t2+t+4),用t分别表示出S△OBF、S△OCF、S△AOC,根据题意列式计算即可.
(1)由题意得,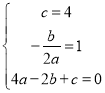 ,
,
解得,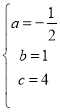 ,
,
则抛物线的解析式为:y=﹣![]() x2+x+4;
x2+x+4;
(2)连接BF、CF、OF,作FG⊥x轴于点G,
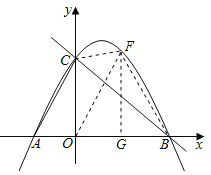
设点F的坐标为(t,﹣![]() t2+t+4),
t2+t+4),
∵A(﹣2,0),抛物线的对称轴是直线 x=1,
∴B(4,0).
∴S△OBF=![]() ×4×(﹣
×4×(﹣![]() t2+t+4)=﹣t2+2t+8,
t2+t+4)=﹣t2+2t+8,
S△OCF=![]() ×4×t=2t,S△AOC=
×4×t=2t,S△AOC=![]() ×2×4=4,
×2×4=4,
∵S四边形ABFC=S△AOC+S△OBF+S△OCF=﹣t2+2t+8,
由题意得,﹣t2+2t+8=15,
解得,t1=1,t2=3,
∴存在点F使四边形ABFC的面积为15,此时,点F的坐标为(1,![]() )或(3,
)或(3,![]() ).
).

【题目】某水果店计划进A,B两种水果共140千克,这两种水果的进价和售价如表所示
进价 | 售价 | |
A种水果 | 5 | 8 |
B种水果 | 9 | 13 |
![]() 若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
![]() 在
在![]() 的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价
的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价![]() 出售,那么售完后共获利多少元?
出售,那么售完后共获利多少元?
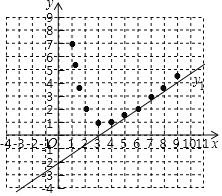
【题目】在平面直角坐标系xOy中,函数y1=![]() x﹣2的图象与函数y2=
x﹣2的图象与函数y2=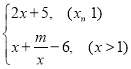 的图象在第一象限有一个交点A,且点A的横坐标是6.
的图象在第一象限有一个交点A,且点A的横坐标是6.
(1)求m的值;
(2)补全表格并以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点,补充画出y2的函数图象;
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 1.2 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y2 | ﹣1 | 1 | 5 | 7 | 5.2 | 3.5 | 2 | 1 | 1 | 2 |
|
|
|
(3)写出函数y2的一条性质: ;
(4)已知函数y1与y2的图象在第一象限有且只有一个交点A,若函数y3=![]() x+n与y2的函数图象有三个交点,求n的取值范围.
x+n与y2的函数图象有三个交点,求n的取值范围.