题目内容
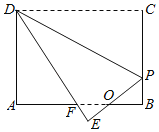
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则BF的长为_____.
【答案】![]()
【解析】
根据折叠的性质可得出DC=DE、CP=EP,由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP,根据全等三角形的性质可得出OE=OB、EF=BP,设BF=EP=CP=x,则AF=4﹣x,BP=3﹣x=EF,DF=DE﹣EF=4﹣(3﹣x)=x+1,依据Rt△ADF中,AF2+AD2=DF2,即可得到x的值.
解:根据折叠可知,DC=DE=4,CP=EP,∠B=∠E=90°,
在△OEF和△OBP中,
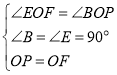 ,
,
∴△OEF≌△OBP(AAS),
∴OE=OB,EF=BP,
∴BF=EP=CP,
设BF=EP=CP=x,则AF=4﹣x,BP=3﹣x=EF,DF=DE﹣EF=4﹣(3﹣x)=x+1,
∵∠A=90°,
∴在Rt△ADF中,AF2+AD2=DF2,
即(4﹣x)2+32=(1+x)2,
解得:x=![]() ,
,
∴BF=![]() ,
,
故答案为:![]() .
.

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?
【题目】在平面直角坐标系xOy中,函数y1=![]() x﹣2的图象与函数y2=
x﹣2的图象与函数y2=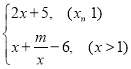 的图象在第一象限有一个交点A,且点A的横坐标是6.
的图象在第一象限有一个交点A,且点A的横坐标是6.
(1)求m的值;
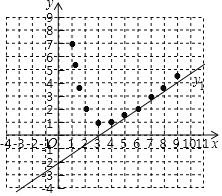
(2)补全表格并以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点,补充画出y2的函数图象;
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 1.2 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y2 | ﹣1 | 1 | 5 | 7 | 5.2 | 3.5 | 2 | 1 | 1 | 2 |
|
|
|
(3)写出函数y2的一条性质: ;
(4)已知函数y1与y2的图象在第一象限有且只有一个交点A,若函数y3=![]() x+n与y2的函数图象有三个交点,求n的取值范围.
x+n与y2的函数图象有三个交点,求n的取值范围.