题目内容
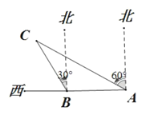
【题目】如图,某渔船在海面上朝正西方向以30海里/小时的速度匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观测到灯塔C在北偏西30°方向上。若该船继续向西航行至离灯塔最近的位置,求此时渔船到灯塔的距离.(结果保留根号)
【答案】渔船到灯塔的距离![]() 海里
海里
【解析】
过点C作CD⊥AB于点D,则若该船继续向西航行至离灯塔距离最近的位置为CD的长度,利用锐角三角函数关系进行求解即可.
如图,过点C作CD⊥AB于点D,
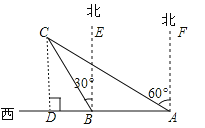
依题意得:AB=30×1=30(海里),
∵∠CAF=60°,∠CBE=30°,
∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,
∴∠ACB=180°﹣∠CBA﹣∠CAB=30°,
∴∠ACB=∠CAB,
∴BC=BA=30(海里),∠CBD=90°﹣∠CBE=60°,
∴CD=BCsin∠CBD=30×![]() =
=![]() (海里).
(海里).
∴渔船到灯塔的距离![]() 海里
海里

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
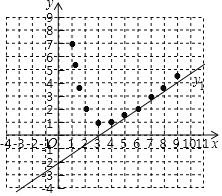
【题目】在平面直角坐标系xOy中,函数y1=![]() x﹣2的图象与函数y2=
x﹣2的图象与函数y2=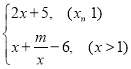 的图象在第一象限有一个交点A,且点A的横坐标是6.
的图象在第一象限有一个交点A,且点A的横坐标是6.
(1)求m的值;
(2)补全表格并以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点,补充画出y2的函数图象;
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 1.2 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y2 | ﹣1 | 1 | 5 | 7 | 5.2 | 3.5 | 2 | 1 | 1 | 2 |
|
|
|
(3)写出函数y2的一条性质: ;
(4)已知函数y1与y2的图象在第一象限有且只有一个交点A,若函数y3=![]() x+n与y2的函数图象有三个交点,求n的取值范围.
x+n与y2的函数图象有三个交点,求n的取值范围.