题目内容
 已知:如图,AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.以下结论:①AD∥OC;②点E为△CDB的内心;③FC=FE;④CE•FB=AB•CF.其中正确的只有
已知:如图,AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.以下结论:①AD∥OC;②点E为△CDB的内心;③FC=FE;④CE•FB=AB•CF.其中正确的只有
- A.①②
- B.②③④
- C.①③④
- D.①②④
D
分析:根据切线长定理,证△COB≌△COD,可得∠COB= ∠BOD,根据圆周角定理即可得出∠DAB=∠COB,由此可证得AD∥OC;
∠BOD,根据圆周角定理即可得出∠DAB=∠COB,由此可证得AD∥OC;
连接DE、BE;上面已证得弧DE=弧BE,根据弦切角定理以及圆周角定理相等,易求得DE、BE分别平分∠CDB和∠CBD;根据三角形内心的定义,即可得出结论②正确;
若FE=FC,则∠OCB=∠CEF=∠OEA=∠OAE,在Rt△OBC中,BD⊥OC,易得∠DBA=∠OCB,即∠DBA=∠EAB;因此弧BE=弧AD,而这个条件并不一定成立.故③不正确;
先证明FB=GB,然后证明△ABG∽△CEF,从而可得出④正确.
解答: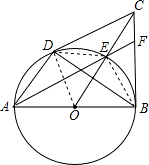 解:连接OD,DE,EB,
解:连接OD,DE,EB,
CD与BC是⊙O的切线,由切线定理知:CD=BC,∠ODC=∠OBC=90°,OD=OB,
∴△CDO≌△CBO,∠COD=∠COB,
∴∠COB=∠DAB= ∠DOB,
∠DOB,
∴AD∥OC,故①正确;
∵CD是⊙O的切线,
∴∠CDE= ∠DOE,而∠BDE=
∠DOE,而∠BDE= ∠BOE,
∠BOE,
∴∠CDE=∠BDE,即DE是∠CDB的角平分线,同理可证得BE是∠CBD的平分线,
因此E为△CBD的内心,故②正确;
若FC=FE,则应有∠OCB=∠CEF,应有∠CEF=∠AEO=∠EAB=∠DBA=∠DEA,
∴弧AD=弧BE,而弧AD与弧BE不一定相等,故③不正确;

设AE、BD 交于点G,由②可知∠EBG=∠EBF,
又∵BE⊥GF,
∴FB=GB,
由切线的性质可得,点E是弧BD的中点,∠DCE=∠BCE,
又∵∠MDA=∠DCE(平行线的性质)=∠DBA,
∴∠BCE=∠GBA,
而∠CFE=∠ABF+∠FAB,∠AGE=∠ADB+∠DAG,∠DAG=∠FAB(等弧所对的圆周角相等),
∴∠AGB=∠CFE,
∴△ABG∽△CEF,
∴CE•GB=AB•CF,
又FB=GB,
∴CE•FB=AB•CF
故④正确.
因此正确的结论有:①②④.
故选D.
点评:本题利用了切线长定理,全等三角形的判定和性质,圆周角定理,弦切角定理,内心的概念,以及对相似三角形的性质求解.
分析:根据切线长定理,证△COB≌△COD,可得∠COB=
 ∠BOD,根据圆周角定理即可得出∠DAB=∠COB,由此可证得AD∥OC;
∠BOD,根据圆周角定理即可得出∠DAB=∠COB,由此可证得AD∥OC;连接DE、BE;上面已证得弧DE=弧BE,根据弦切角定理以及圆周角定理相等,易求得DE、BE分别平分∠CDB和∠CBD;根据三角形内心的定义,即可得出结论②正确;
若FE=FC,则∠OCB=∠CEF=∠OEA=∠OAE,在Rt△OBC中,BD⊥OC,易得∠DBA=∠OCB,即∠DBA=∠EAB;因此弧BE=弧AD,而这个条件并不一定成立.故③不正确;
先证明FB=GB,然后证明△ABG∽△CEF,从而可得出④正确.
解答:
 解:连接OD,DE,EB,
解:连接OD,DE,EB,CD与BC是⊙O的切线,由切线定理知:CD=BC,∠ODC=∠OBC=90°,OD=OB,
∴△CDO≌△CBO,∠COD=∠COB,
∴∠COB=∠DAB=
 ∠DOB,
∠DOB,∴AD∥OC,故①正确;
∵CD是⊙O的切线,
∴∠CDE=
 ∠DOE,而∠BDE=
∠DOE,而∠BDE= ∠BOE,
∠BOE,∴∠CDE=∠BDE,即DE是∠CDB的角平分线,同理可证得BE是∠CBD的平分线,
因此E为△CBD的内心,故②正确;
若FC=FE,则应有∠OCB=∠CEF,应有∠CEF=∠AEO=∠EAB=∠DBA=∠DEA,
∴弧AD=弧BE,而弧AD与弧BE不一定相等,故③不正确;

设AE、BD 交于点G,由②可知∠EBG=∠EBF,
又∵BE⊥GF,
∴FB=GB,
由切线的性质可得,点E是弧BD的中点,∠DCE=∠BCE,
又∵∠MDA=∠DCE(平行线的性质)=∠DBA,
∴∠BCE=∠GBA,
而∠CFE=∠ABF+∠FAB,∠AGE=∠ADB+∠DAG,∠DAG=∠FAB(等弧所对的圆周角相等),
∴∠AGB=∠CFE,
∴△ABG∽△CEF,
∴CE•GB=AB•CF,
又FB=GB,
∴CE•FB=AB•CF
故④正确.
因此正确的结论有:①②④.
故选D.
点评:本题利用了切线长定理,全等三角形的判定和性质,圆周角定理,弦切角定理,内心的概念,以及对相似三角形的性质求解.

练习册系列答案
相关题目
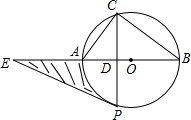 (2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA=
(2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA=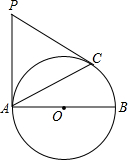 已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°. 已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为
已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为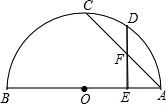 已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①
已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①
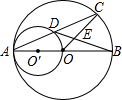 已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.
已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.