题目内容
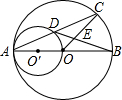 已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.
已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.
分析:连接OD、BC,根据圆周角定理知OD、BC都与AC垂直,因此OD∥BC,而AO=OB,即OD是△ABC的中位线,因此OD:BC=1:2,易证得△OED∽△CEB,根据OD、BC的比例关系知:两个三角形的相似比为1:2,可得EC=2OE、BE=2DE,欲求CE、DE,必须先求出OC、BD的长;已知了⊙O的直径AB的长,即可得到半径OC的长,根据CE、OC的比例关系即可求出CE的值;在Rt△OAD和Rt△ABC中,通过解直角三角形,可求出AD、BC的长,由于OD⊥AC,根据垂径定理可得到CD的长,那么在Rt△BCD中,通过勾股定理即可求得BD的值,根据DE、BD的比例关系,可得到DE的长,由此得解.
解答: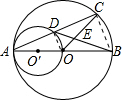 解法一:连接OD、BC,(1分)
解法一:连接OD、BC,(1分)
∵AO、AB分别是⊙O'和⊙O的直径,
∴∠ADO=∠ACB=90°,且AD=DC,(2分)
∴OD∥BC,BC=2OD,(3分)
∴△OED∽△CEB,
∴
=
=
=
,(5分)
∴
=
,CE=
OC=
AB=
,(6分)
在Rt△AOD和Rt△ABC中,∠OAD=30°,AB=4,
∴BC=2OD=
AB=2,
AC=AB•cos30°=2
,(8分)
∴AD=CD=
,
又在Rt△BDC中,BD=
=
,
∴DE=
BD=
.(9分)
解法二:同解法一证得AD=DC,(2分)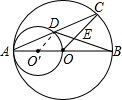
可再连接O'D,则O'D∥OC,(3分)
∴
=
=2,
=
=
,(4分)
∴DE=
BD,OE=
O′D=
,(6分)
以下同解法一.
 解法一:连接OD、BC,(1分)
解法一:连接OD、BC,(1分)∵AO、AB分别是⊙O'和⊙O的直径,
∴∠ADO=∠ACB=90°,且AD=DC,(2分)
∴OD∥BC,BC=2OD,(3分)
∴△OED∽△CEB,
∴
| DE |
| BE |
| OE |
| CE |
| OD |
| BC |
| 1 |
| 2 |
∴
| DE |
| BD |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
在Rt△AOD和Rt△ABC中,∠OAD=30°,AB=4,
∴BC=2OD=
| 1 |
| 2 |
AC=AB•cos30°=2
| 3 |
∴AD=CD=
| 3 |
又在Rt△BDC中,BD=
| BC2+CD2 |
| 7 |
∴DE=
| 1 |
| 3 |
| ||
| 3 |
解法二:同解法一证得AD=DC,(2分)

可再连接O'D,则O'D∥OC,(3分)
∴
| BE |
| DE |
| BO |
| 00′ |
| OE |
| O′D |
| BO |
| BO′ |
| 2 |
| 3 |
∴DE=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
以下同解法一.
点评:此题主要考查了圆周角定理、三角形中位线定理、解直角三角形以及相似三角形的性质等知识,能够得到DE、BE以及CE、OE的比例关系是解答此题的关键.

练习册系列答案
相关题目
 (2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA=
(2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA= 已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°. 已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为
已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为 已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①
已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①