题目内容
 (2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA=
(2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA=| 3 |
(1)求PC的长;
(2)过P作⊙O切线交BA延长线于E,求图中阴影部分的面积.
分析:(1)由弧AC=弧AP,根据垂径定理可得AB⊥CP,AD=PD=
PC,由AB为⊙O的直径,根据直径所对的圆周角是直角,可求得∠ACB=90°,由tanA=
,可得∠BAC=60°,由三角函数可求得AC的长,继而求得答案;
(2)首先连接OP,可求得△OPE的面积与扇形AOP的面积,继而求得答案.
| 1 |
| 2 |
| 3 |
(2)首先连接OP,可求得△OPE的面积与扇形AOP的面积,继而求得答案.
解答:解:(1)∵
=
,
∴AB⊥CP,AD=PD=
PC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵tanA=
.
∴∠BAC=60°,
∴AC=AB•cos60°=5,
∴CD=AC•sin60°=
,
∴PC=5
;
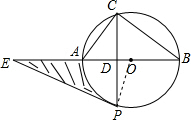 (2)连接OP,
(2)连接OP,
∵PE是⊙O的切线,
∴OP⊥PE,
∵∠BAC=60°,
∴∠ACP=90°-∠BAC=30°,
∴∠AOP=2∠ACP=60°,
∵OP=
AB=5,
∴PE=OP•tan60°=5
,
∴S△OPE=
OP•PE=
,S扇形AOP=
π×52=
π,
∴S阴影=S△OPE-S扇形AOP=
-
π.
 |
| AC |
 |
| AP |
∴AB⊥CP,AD=PD=
| 1 |
| 2 |
∵AB为⊙O的直径,
∴∠ACB=90°,
∵tanA=
| 3 |
∴∠BAC=60°,
∴AC=AB•cos60°=5,
∴CD=AC•sin60°=
5
| ||
| 2 |
∴PC=5
| 3 |
 (2)连接OP,
(2)连接OP,∵PE是⊙O的切线,
∴OP⊥PE,
∵∠BAC=60°,
∴∠ACP=90°-∠BAC=30°,
∴∠AOP=2∠ACP=60°,
∵OP=
| 1 |
| 2 |
∴PE=OP•tan60°=5
| 3 |
∴S△OPE=
| 1 |
| 2 |
25
| ||
| 2 |
| 60 |
| 360 |
| 25 |
| 6 |
∴S阴影=S△OPE-S扇形AOP=
| 25 |
| 2 |
| 3 |
| 25 |
| 6 |
点评:此题考查了切线的性质、扇形的面积以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 (2013•东阳市模拟)如图,C、D、B的坐标分别为(1,0)(9,0)(10,0),点P(t,0)是CD上一个动点,在x轴上方作等边△OPE和△BPF,连EF,G为EF的中点.
(2013•东阳市模拟)如图,C、D、B的坐标分别为(1,0)(9,0)(10,0),点P(t,0)是CD上一个动点,在x轴上方作等边△OPE和△BPF,连EF,G为EF的中点.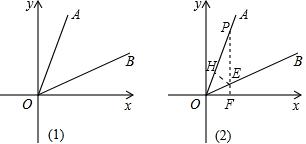
 (2013•东阳市模拟)如图,平面直角坐标系中,点A(0,4),B(3,0),D、E在x轴上,F为平面上一点,且EF⊥x轴,直线DF与直线AB互相垂直,垂足为H,△AOB≌△DEF,设BD=h.
(2013•东阳市模拟)如图,平面直角坐标系中,点A(0,4),B(3,0),D、E在x轴上,F为平面上一点,且EF⊥x轴,直线DF与直线AB互相垂直,垂足为H,△AOB≌△DEF,设BD=h.