题目内容
 已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为
已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为130°
130°
.分析:首先连接BC,由AB为⊙O直径,根据半圆(或直径)所对的圆周角是直角,即可求得∠ACB的度数,又由直角三角形中两锐角互余,即可求得∠B的度数,然后根据圆的内接四边形的性质,即可求得∠AMC的度数.
解答: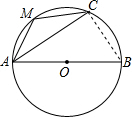 解:连接BC,
解:连接BC,
∵AB为⊙O直径,
∴∠ACB=90°,
∵∠CAB=40°,
∴∠B=90°-∠CAB=50°,
∵四边形ABCM是⊙O的内接四边形,
∴∠AMC+∠B=180°,
∴∠AMC=180°-∠B=130°.
故答案为:130°.
 解:连接BC,
解:连接BC,∵AB为⊙O直径,
∴∠ACB=90°,
∵∠CAB=40°,
∴∠B=90°-∠CAB=50°,
∵四边形ABCM是⊙O的内接四边形,
∴∠AMC+∠B=180°,
∴∠AMC=180°-∠B=130°.
故答案为:130°.
点评:此题考查了圆周角定理、圆的内接四边形的性质以及直角三角形的性质.此题难度适中,解题的关键是准确作出辅助线,掌握直径所对的圆周角是直角与圆内接四边形的对角互补定理的应用.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 (2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA=
(2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA= 已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°. 已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①
已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①
 已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.
已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.