题目内容
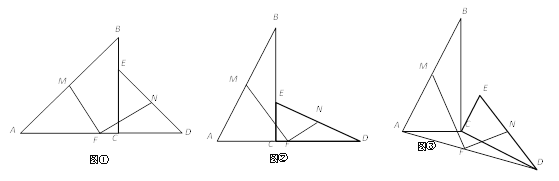
【题目】已知如图①Rt△ABC和Rt△EDC中,∠ACB=∠ECD=90°,A,C,D在同一条直线上,点M,N,F分别为AB,ED,AD的中点,∠B=∠EDC=45°,
(1)求证MF=NF
(2)当∠B=∠EDC=30°,A,C,D在同一条直线上或不在同一条直线上,如图②,图③这两种情况时,请猜想线段MF,NF之间的数量关系。(不必证明)
【答案】(1)见解析;(2)MF=![]() NF.
NF.
【解析】
(1)连接AE,BD,先证明△ACE和△BCD全等,然后得到AE=BD,然后再通过三角形中位线证明即可.
(2)根据图(2)(3)进行合理猜想即可.
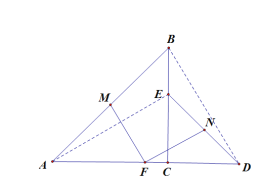
解:(1)连接AE,BD
在△ACE和△BCD中

∴△ACE≌△BCD
∴AE=BD
又∵点M,N,F分别为AB,ED,AD的中点
∴MF=![]() BD,NF=
BD,NF=![]() AE
AE
∴MF=NF
(2) MF=![]() NF.
NF.
方法同上.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量y与单价x满足一次函数关系,求出y与x的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?