题目内容
【题目】如图，在直角坐标系中，直线y1=2x﹣2与坐标轴交于A、B两点，与双曲线y2= 
（x＞0）交于点C，过点C作CD⊥x轴，且OA=AD，则以下结论： ①当x＞0时，y1随x的增大而增大，y2随x的增大而减小；
②k=4；
③当0＜x＜2时，y1＜y2；
④如图，当x=4时，EF=4．
其中正确结论的个数是（ ）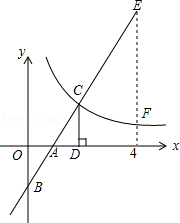
A.1
B.2
C.3
D.4
【答案】C
【解析】解：对于直线y1=2x﹣2， 令x=0，得到y=2；令y=0，得到x=1，
∴A（1，0），B（0，﹣2），即OA=1，OB=2，
在△OBA和△CDA中，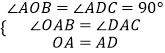 
，
∴△OBA≌△CDA（AAS），
∴CD=OB=2，OA=AD=1，
∴C（2，2），
当x＞0时，y1随x的增大而增大，y2随x的增大而减小；故①正确；
把C坐标代入反比例解析式得：k=4，故②正确；
由函数图象得：当0＜x＜2时，y1＜y2 ， 选项③正确；
当x=4时，y1=6，y2=1，即EF=6﹣1=5，选项④错误；
故选C
对于直线解析式，分别令x与y为0求出y与x的值，确定出A与B坐标，利用AAS得到三角形OBA与三角形CDA全等，利用全等三角形对应边相等得到CD=OB，确定出C坐标，代入反比例解析式求出k的值，确定出反比例解析式，由图象判断y1＜y2时x的范围，以及y1与y2的增减性，把x=2分别代入直线与反比例解析式，相减求出EF的长，即可做出判断．
练习册系列答案
相关题目
