题目内容
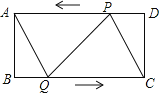
【题目】如图，在矩形ABCD中，
，
点P从点D出发向点A运动，运动到点A即停止；同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是
，连接PQ、AQ、
设点P、Q运动的时间为ts．
当t为何值时，四边形ABQP是矩形；
当t为何值时，四边形AQCP是菱形．
【答案】
当
时，四边形ABQP为矩形；
当
时，四边形AQCP为菱形．
【解析】
当四边形ABQP是矩形时，
，据此求得t的值；
当四边形AQCP是菱形时，
，列方程求得运动的时间t；
由已知可得，
，
在矩形ABCD中，
，
，
当时，四边形ABQP为矩形，
，得
故当时，四边形ABQP为矩形．
由可知，四边形AQCP为平行四边形
当
时，四边形AQCP为菱形
即
时，四边形AQCP为菱形，解得
，
故当时，四边形AQCP为菱形．
练习册系列答案
相关题目
