题目内容
如图,已知抛物线y=x2+bx+c的顶点坐标为M(0,﹣1),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)判断△MAB的形状,并说明理由;
(3)过原点的任意直线(不与y轴重合)交抛物线于C、D两点,连接MC,MD,试判断MC、MD是否垂直,并说明理由.
(1)抛物线的解析式为:y=x2﹣1;
(2)△MAB是等腰直角三角形,理由见解析;
(3)MC⊥MF,理由见解析.
解析试题分析:(1)待定系数法即可解得.
(2)由抛物线的解析式可知OA=OB=OC=1,得出∠AMO=∠MAO=∠BMO=∠BOM=45°从而得出△MAB是等腰直角三角形.
(3)分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC于G,交DF于H,设D(m,m2﹣1),C(n,n2﹣1),通过FG∥DH,得出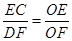 ,从而求得m、n的关系,根据m、n的关系,得出△CGM∽△MHD,即可求得结论.
,从而求得m、n的关系,根据m、n的关系,得出△CGM∽△MHD,即可求得结论.
试题解析:(1)∵抛物线y=x2+bx+c的顶点坐标为M(0,﹣1),
∴b=0,c=﹣1,
∴抛物线的解析式为:y=x2﹣1;
(2)△MAB是等腰直角三角形,
由抛物线的解析式为:y=x2﹣1可知A(﹣1,0),B(1,0),
∴OA=OB=OC=1,
∴∠AMO=∠MAO=∠BMO=∠BOM=45°,
∴∠AMB=∠AMO+∠BMO=90°
∵y轴是对称轴,
∴A、B为对称点,
∴AM=BM,
∴△MAB是等腰直角三角形;
(3)MC⊥MF;分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC于G,交DF于H,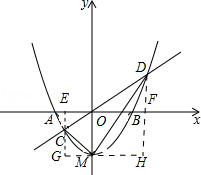
设D(m,m2﹣1),C(n,n2﹣1),
∴OE=﹣n,CE=1﹣n2,OF=m,DF=m2﹣1,
∵OM=1,
∴CG=n2,DH=m2,
∵FG∥DH,
∴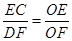 ,
,
即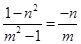
解得m=﹣ ,
,
又∵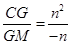 =﹣n,
=﹣n,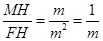 ,
,
∴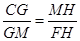 ,
,
∵∠CGM=∠MHD=90°,
∴△CGM∽△MHD,
∴∠CMG=∠MDH,
∵∠MDH+∠DMH=90°
∴∠CMG+∠DMH=90°,
∴∠CMD=90°,
即MC⊥MF.
考点:二次函数综合题.

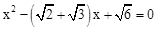 的根是
的根是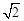 和
和 .
. ,则CD=3.
,则CD=3. 的图象上,则k=﹣1.
的图象上,则k=﹣1.
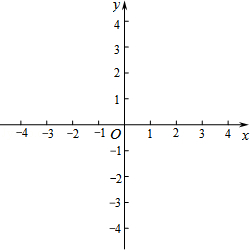
 与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC. 的值;
的值; 中,二次函数
中,二次函数 的图像与
的图像与 轴交于点A,B(点B在点A的左侧),与
轴交于点A,B(点B在点A的左侧),与 轴交于点C,过动点H(0,
轴交于点C,过动点H(0,  )作平行于
)作平行于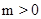 ,以DE为直径作⊙Q,当⊙Q与
,以DE为直径作⊙Q,当⊙Q与
 ,
, (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式; ,试求出t的取值范围.
,试求出t的取值范围. 经过点A(3,2),B(0,1)和点C
经过点A(3,2),B(0,1)和点C .
. ,求点F的坐标;
,求点F的坐标;
