题目内容
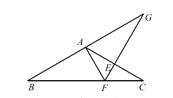
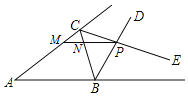
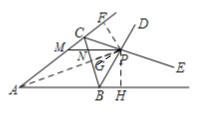
【题目】如图△ABC 的∠ABC 的外角平分线 BD 与∠ACB 的外角平分线 CE 交于 P,过 P 作 MN∥AB 交 AC 于M,交 BC 于 N,且 AM=8,BN=5,则 MN=( )
A. 2B. 3C. 4D. 5
【答案】B
【解析】
过P作PF⊥AC,PG⊥BC,PH⊥AB,连接AP,依据条件可得AP平分∠BAC,再根据平行线的性质和角平分线定义得出∠MAP=∠MPA,∠NBP=∠NPB,即可得到AM=PM,NP=NB,再根据MN=MP-NP=AM-BN进行计算即可.
如图,过P作PF⊥AC,PG⊥BC,PH⊥AB,连接AP,
∵∠ABC的外角平分线BD与∠ACB的外角平分线CE交于P,
∴PF=PG=PH,
∴点P在∠BAC的平分线上,即AP平分∠BAC,
∴∠MAP=∠BAP,
∵MN∥AB,
∴∠BAP=∠MPA,
∴∠MAP=∠MPA,
∴AM=PM,
同理可得:∠NBP=∠NPB,
∴NP=NB,
∴MN=MP-NP=AM-BN=8-5=3,
故选:B.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案【题目】已知y=ax2+bx+c(其中a,b,c为常数,且a≠0),乐老师在用描点法画其的图象时,列出如下表格,根据该表格,下列判断中不正确的是( )
x | … | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣2 | 2.5 | 4 | 2.5 | … |
A. a<0
B. 一元二次方程ax2+bx+c﹣5=0没有实数根
C. 当x=3时y=﹣2
D. 一元二次方程ax2+bx+c=0有一根比3大
【题目】小山同学结合学习一次函数的经验和自己的思考,按以下方式探究函数![]() 的图象与性质,并尝试解决相关问题.
的图象与性质,并尝试解决相关问题.
请将以下过程补充完整:
(1)判断这个函数的自变量x的取值范围是________________;
(2)补全表格:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
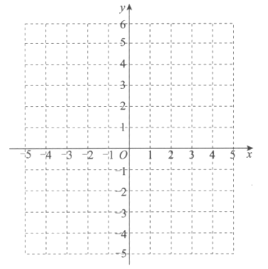
(3)在平面直角坐标系![]() 中画出函数
中画出函数![]() 的图象:
的图象:
(4)填空:当![]() 时,相应的函数解析式为___(用不含绝对值符合的式子表示);
时,相应的函数解析式为___(用不含绝对值符合的式子表示);
(5)写出直线![]() 与函数
与函数![]() 的图象的交点坐标.
的图象的交点坐标.