题目内容
【题目】小山同学结合学习一次函数的经验和自己的思考,按以下方式探究函数![]() 的图象与性质,并尝试解决相关问题.
的图象与性质,并尝试解决相关问题.
请将以下过程补充完整:
(1)判断这个函数的自变量x的取值范围是________________;
(2)补全表格:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
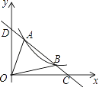
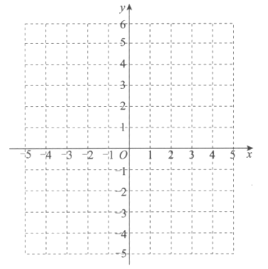
(3)在平面直角坐标系![]() 中画出函数
中画出函数![]() 的图象:
的图象:
(4)填空:当![]() 时,相应的函数解析式为___(用不含绝对值符合的式子表示);
时,相应的函数解析式为___(用不含绝对值符合的式子表示);
(5)写出直线![]() 与函数
与函数![]() 的图象的交点坐标.
的图象的交点坐标.
【答案】(1)全体实数;(2)见解析;(3)见解析;(4)![]() ;(5)
;(5)![]()
【解析】
(1)由函数解析式:![]() 可以得到自变量
可以得到自变量![]() 的取值范围,
的取值范围,
(2)利用函数解析式给出的自变量的值得出函数值可以得到答案.
(3)根据自变量与函数值的对应值在平面直角坐标系中描好点并连线得到图像.
(4)在![]() 的条件下去掉绝对值符号,得到函数解析式.
的条件下去掉绝对值符号,得到函数解析式.
(5)观察图像写出交点坐标即可.
(1)因为:![]() ,所以函数自变量的取值范围是全体实数.
,所以函数自变量的取值范围是全体实数.
(2)利用![]() 把
把![]() 分别代入解析式计算出函数
分别代入解析式计算出函数![]() 的值填入下表:
的值填入下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
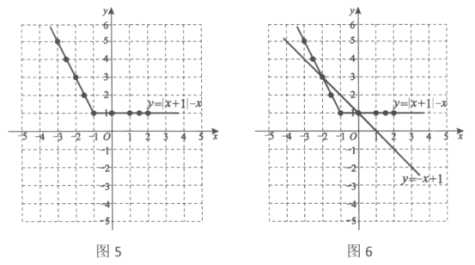
(3)描点并连线(见图5).
(4)因为:![]() ,所以
,所以![]()
所以:![]()
(5)在同一直角坐标系中画出![]() 的图像,观察图像得交点为
的图像,观察图像得交点为![]() (如图6所示).
(如图6所示).

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.