题目内容
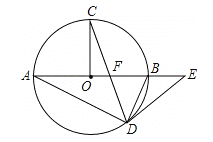
【题目】如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若tanA=![]() ,探究线段AB和BE之间的数量关系,并证明;
,探究线段AB和BE之间的数量关系,并证明;
(3)在(2)的条件下,若OF=1,求圆O的半径.
【答案】(1)答案见解析;(2)AB=3BE;(3)3.
【解析】试题分析:(1)先判断出∠OCF+∠CFO=90°,再判断出∠OCF=∠ODF,即可得出结论;
(2)先判断出∠BDE=∠A,进而得出△EBD∽△EDA,得出AE=2DE,DE=2BE,即可得出结论;
(3)设BE=x,则DE=EF=2x,AB=3x,半径OD=![]() x,进而得出OE=1+2x,最后用勾股定理即可得出结论.
x,进而得出OE=1+2x,最后用勾股定理即可得出结论.
试题解析:(1)证明:连结OD,如图.∵EF=ED,∴∠EFD=∠EDF.∵∠EFD=∠CFO,∴∠CFO=∠EDF.∵OC⊥OF,∴∠OCF+∠CFO=90°.∵OC=OD,∴∠OCF=∠ODF,∴∠ODC+∠EDF=90°,即∠ODE=90°,∴OD⊥DE.∵点D在⊙O上,∴DE是⊙O的切线;
(2)线段AB、BE之间的数量关系为:AB=3BE.证明如下:
∵AB为⊙O直径,∴∠ADB=90°,∴∠ADO=∠BDE.∵OA=OD,∴∠ADO=∠A,∴∠BDE=∠A,而∠BED=∠DEA,∴△EBD∽△EDA,∴![]() .∵Rt△ABD中,tanA=
.∵Rt△ABD中,tanA=![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
∴AE=2DE,DE=2BE,∴AE=4BE,∴AB=3BE;
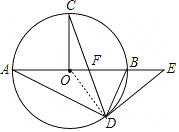
(3)设BE=x,则DE=EF=2x,AB=3x,半径OD=![]() x.∵OF=1,∴OE=1+2x.
x.∵OF=1,∴OE=1+2x.
在Rt△ODE中,由勾股定理可得:(![]() x)2+(2x)2=(1+2x)2,∴x=﹣
x)2+(2x)2=(1+2x)2,∴x=﹣![]() (舍)或x=2,∴圆O的半径为3.
(舍)或x=2,∴圆O的半径为3.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目