题目内容
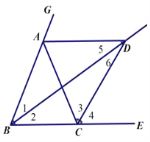
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

【答案】(1)证明见解析;(2)证明见解析;(3)∠BDC=![]() ∠BAC,证明见解析
∠BAC,证明见解析
【解析】
(1)根据平行线的性质得到∠ADB=∠DBC,由角平分线的定义得到∠ABD=∠DBC,等量代换得到∠ABD=∠ADB,根据等腰三角形的判定即可得到AB=AD;(2)根据平行线的性质得到∠ADC=∠DCE,由①知AB=AD,等量代换得到AC=AD,根据等腰三角形的性质得到∠ACD=∠ADC,求得∠ACD=∠DCE,即可得到结论;
(3)根据角平分线的定义得到∠DBC=![]() ∠ABC,∠DCE=
∠ABC,∠DCE=![]() ∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+
∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+![]() ∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠BDC+
∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠BDC+![]() ∠ABC=
∠ABC=![]() ∠ABC+
∠ABC+![]() ∠BAC,即可得到结论.
∠BAC,即可得到结论.
证明:
![]() (1) AD∥BE
(1) AD∥BE
![]() ∠2= ∠5
∠2= ∠5
![]() AD平分∠GBE
AD平分∠GBE
![]() ∠2= ∠1
∠2= ∠1
![]() ∠1= ∠5 , AB= AD
∠1= ∠5 , AB= AD
(2) ![]() AB= AD AB= ACAC= AD
AB= AD AB= ACAC= AD
![]() ∠3= ∠ADC
∠3= ∠ADC
![]() 又AD∥BE ∠ADC= ∠4
又AD∥BE ∠ADC= ∠4
![]() ∠3= ∠4
∠3= ∠4
![]() CD平分∠ACE
CD平分∠ACE
(3)∠BDC=![]() ∠BAC
∠BAC
![]()
![]() 证明:BD平分∠ABE
证明:BD平分∠ABE
∴∠2= ∠1 = ![]() ∠ABC
∠ABC
∠1+ ∠2+ ∠BAC=∠4 +∠3①
①式两边除以2得![]() ∠BAC=∠4-∠2
∠BAC=∠4-∠2
而由∠2+ ∠6 =∠4 得出∠6 =∠4 -∠2 即∠BDC=∠4 -∠2
∠BDC=![]() ∠BAC
∠BAC

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目