��Ŀ����
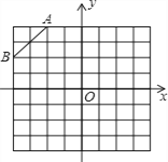
����Ŀ����ͼ�ǹ��Ϊ8��8��������������������������������Ҫ�������
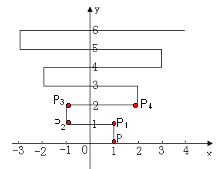
��1���ڵڶ������ڵĸ������һ��C�� ʹ��C���߶�AB���һ����ABΪ�ĵ��������Σ� ���������������� ��C��������____________����ABC�������_____________________��
��2��������ABC���Ե�CΪ��ת���ġ���ת180������A��B��C������AB����A��B�� ���ı���AB A��B������״�Ǻ������ı��Σ�___________________��
��3�������������Ƿ����P�㣬ʹ�á�PAB���CAB�������ȣ������ڣ���ֱ��д����P�����꣨д��һ��������ɣ�___________________��
���𰸡� C��-1,1�� 4 ���� P��0,2����-2,0��
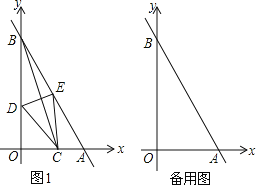
����������������1��������������ѡ�ɣ��𰸲�Ψһ�������ù��ɶ�������֤����Ϊ���������ø�������ABC�������
��2��������ת180������ԭͼ�γ����ĶԳƣ������ӳ�AC��BD��ʹ![]() ,
,![]() ,���ɻ���ͼ�Σ�Ȼ����ݾ��ε��ж�����˵�����ɣ�
,���ɻ���ͼ�Σ�Ȼ����ݾ��ε��ж�����˵�����ɣ�
��3��������������ѡ��Ȼ����������֤.
��⣺��1����ͼ��ȡ��C��-1,1������AC=BC=![]() ��
��
��ABC�����=4��4-![]() ��
��
��2���ӳ�AC��BD��ʹ![]() ,
,![]() ������AB����A��B��B���B��
������AB����A��B��B���B��
�������֪��BC=CB�䣬AC=CA�䣬
���ı���ABA��B����ƽ���ı��Σ�
�֡�AA��=BB�䣬
���ı���ABA��B���Ǿ�����
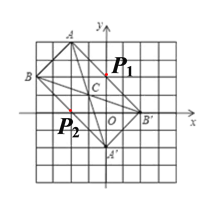
��3����ͼ����P1��0,2��ʱ��
S��ABP1=![]() ,�������⣻
,�������⣻
��P2��-2,0��ʱ��
S��ABP1=![]() ,�������⣻
,�������⣻
��P�������ǣ�0,2����-2,0��.

 ����������������ϵ�д�
����������������ϵ�д�