题目内容
【题目】如图1,已知直线y=﹣2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连接BC,作BC的中垂线分别交OB、AB交于点D、E.
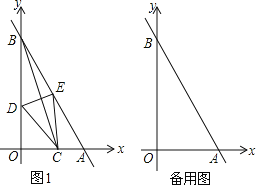
(l)当点C与点O重合时,DE= ;
(2)当CE∥OB时,证明此时四边形BDCE为菱形;
(3)在点C的运动过程中,直接写出OD的取值范围.
【答案】(1)1;(2)证明详见解析;(3)![]() ≤OD≤2.
≤OD≤2.
【解析】
试题分析:(1)画出图形,根据DE垂直平分BC,可得出DE是△BOA的中位线,从而利用中位线的性质求出DE的长度;
(2)先根据中垂线的性质得出DB=DC,EB=EC,然后结合CE∥OB判断出BE∥DC,得出四边形BDCE为平行四边形,结合DB=DC可得出结论.
(3)求两个极值点,①当点C与点A重合时,OD取得最小值,②当点C与点O重合时,OD取得最大值,继而可得出OD的取值范围.
试题解析:解:∵直线AB的解析式为y=﹣2x+4,
∴点A的坐标为(2,0),点B的坐标为(0,4),即可得OB=4,OA=2,
(1)当点C与点O重合时如图所示,
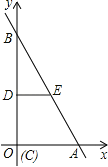
∵DE垂直平分BC(BO),
∴DE是△BOA的中位线,
∴DE=![]() OA=1;
OA=1;
(2)当CE∥OB时,如图所示:
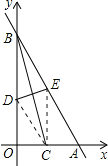
∵DE为BC的中垂线,
∴BD=CD,EB=EC,
∴∠DBC=∠DCB,∠EBC=∠ECB,
∴∠DCE=∠DBE,
∵CE∥OB,
∴∠CEA=∠DBE,
∴∠CEA=∠DCE,
∴BE∥DC,
∴四边形BDCE为平行四边形,
又∵BD=CD,
∴四边形BDCE为菱形.
(3)当点C与点O重合时,OD取得最大值,此时OD=![]() OB=2;
OB=2;
当点C与点A重合时,OD取得最小值,如图所示:
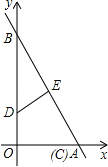
在Rt△AOB中,AB=![]() =2
=2![]() ,
,
∵DE垂直平分BC(BA),
∴BE=![]() BA=
BA=![]() ,
,
易证△BDE∽△BAO,
∴![]() ,即
,即![]() ,
,
解得:BD=![]() ,
,
则OD=OB﹣BD=4﹣![]() =
=![]() .
.
综上可得:![]() ≤OD≤2.
≤OD≤2.