Question

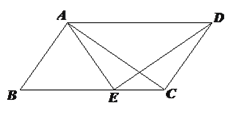
【题目】如图，在四边形ABCD中，AB//CD，∠B=∠ADC，点E是BC边上的一点，且AE=DC．

（1）求证：△ABC≌△EAD ；

（2）如果AB⊥AC，求证：∠BAE= 2∠ACB．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）易证△ABC≌△CDA得BC=AD，AB=DC，∠ACB=∠CAD；再证∠B=∠EAD；进而再证明AB=AE，即可得证；

（2）过点A作AH⊥BC于H ，利用等腰三角形的三线合一的性质和直角三角形两锐角互余即可得证.

试题解析：（1）∵ AB//CD，

∴ ∠BAC=∠DCA .

又 ∠B=∠ADC，AC=CA，

∴ △ABC≌△CDA .

∴ BC=AD，AB=DC，∠ACB=∠CAD .

又 AE=DC，AB=DC，

∴ AB=AE .

∴ ∠B=∠AEB .

又 ∠ACB=∠CAD，

∴ AD//BC，

∴ ∠AEB=∠EAD .

∴ ∠B=∠EAD .

在△ABC与△EAD中，

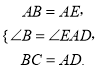
∴ △ABC≌△EAD .

（2）过点A作AH⊥BC于H .

∵ AB=AE，AH⊥BC .

∴ ∠BAE=2∠BAH .

在△ABC中，

∵ ∠BAC+∠B+∠ACB=180°，

又 AB⊥AC，∴ ∠BAC=90°.

∴ ∠B+∠ACB=90°.

同理：∠B+∠BAH=90°.

∴ ∠BAH=∠ACB .

∴ ∠BAE=2∠ACB .