题目内容
【题目】如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
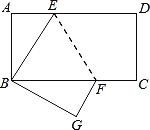
(1)试判断△BEF的形状,并说明理由;
(2)若AE=3,求△BEF的面积.
【答案】(1)△BEF为等腰三角形,理由见解析;(2)10
【解析】
(1)根据平行线的性质可得:∠DEF=∠EFB,然后根据折叠的性质可得∠DEF=∠BEF,从而证出∠BEF=∠EFB,最后根据等角对等边可证BE=BF,从而得出结论.
(2)根据矩形的性质可得:∠A=90°,然后根据勾股定理即可求出BF=BE=5,最后根据三角形的面积公式计算即可.
解:(1)如图,△BEF为等腰三角形;理由如下:
∵AD∥BC,
∴∠DEF=∠EFB
由折叠的性质可得:∠DEF=∠BEF,
∴∠BEF=∠EFB,
∴BE=BF,
∴△BEF为等腰三角形.
(2)∵四边形ABCD为矩形,
∴∠A=90°,
∵BE=![]() =
=![]() =5,
=5,
∴BF=BE=5,
∴△BEF的面积=![]() ×BF×AB=10.
×BF×AB=10.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目